
分析 分当A是直角三角形的直角顶点时,当C在AB的下侧或上侧;以及当B是直角三角形的直角顶点时,当C在AB的下侧或上侧;以及当C是直角三角形的直角顶点时,当C在AB的下侧或上侧共6种情况进行讨论,利用全等三角形的判定与性质以及相似三角形的性质即可求解.
解答 解:1)当A是直角三角形的直角顶点时,当C在AB的下侧时,设是C1,作BD⊥y轴于点D,作C1E⊥y轴于点D.
∵∠C1AE+∠BAD=90°,
又∵直角△AC1E中,∠C1AE+∠C1=90°,
∴∠C1=∠BAD,
在△AC1E和△BAD中,$\left\{\begin{array}{l}{∠{C}_{1}=∠BAC}\\{∠AE{C}_{1}=∠ADB}\\{AB=A{C}_{1}}\end{array}\right.$,
∴△AC1E≌△BAD,
∴C1E=AD,AE=BD,
∵A(0,6),B(8,3),
∴C1E=AD=6-3=3,AE=BD=8,
∴OE=AE-OA=8-6=2,
∴C1的坐标是(-3,-2);
2)当A是直角三角形的直角顶点时,当C在AB的下侧时,设是C2,此时与C1关于A对称,则C2的坐标是:(3,14);
3)当B是直角三角形的直角顶点,当C在AB的下侧时,设是C3,作C3F⊥BD于点F,同1)可得:△AC1E≌△C3FB,
则BF=C1E=3,C3F=AE=8,
则C3的坐标是:(5,-5);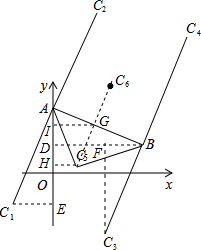
4)当B是直角三角形的直角顶点,当C在AB的上侧时,设是C4,
则B是C3C4的中点,设C4的坐标是(x,y),则$\frac{3+x}{2}$=8,$\frac{-5+y}{2}$=3,
解得:x=13,y=11,
则C4的坐标是(13,11);
5)当C是直角顶点,则C一定在AB的中垂线上,在AB的下方时,设为C5,作C5H⊥y轴于H,过AB的中点G作GI⊥y轴于点I.
则△AHC5∽△GIA,且相似比是:$\frac{A{C}_{5}}{AG}$=$\sqrt{2}$,GI=4,
∴$\frac{AH}{IG}$=$\frac{HG}{AI}$=$\sqrt{2}$,
∴AH=$\sqrt{2}$IG=4$\sqrt{2}$,
∴OH=OA-AH=6-4$\sqrt{2}$,HG=$\sqrt{2}$AI=$\frac{3\sqrt{2}}{2}$,
∴C5的坐标是:($\frac{3\sqrt{2}}{2}$,6-4$\sqrt{2}$);
6)当C是直角顶点,则C一定在AB的中垂线上,在AB的上方时,设是C6,C5和C6关于G(4,$\frac{9}{2}$)对称,方法同4)即可求得C6的坐标是($\frac{16-3\sqrt{2}}{2}$,3+4$\sqrt{2}$).
总之,C的坐标是:(-3,-2)或(3,14)或(5,-5)或(13,11)或($\frac{3\sqrt{2}}{2}$,6-4$\sqrt{2}$)或($\frac{16-3\sqrt{2}}{2}$,3+4$\sqrt{2}$).
点评 本题考查了全等三角形的判定与性质,相似三角形的判定与性质,正确进行讨论是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
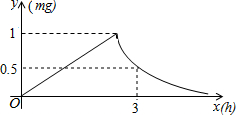 为了预防流感,某校在休息日用药熏消毒法对教室进行消毒,消毒过程中,室内每立方米空气中的含药量y(mg)与消毒开始后的时间x(h)之间的函数图象如图所示,其中药物释放完毕前y与x成正比例;药物释放完毕后,y与x成反比例.
为了预防流感,某校在休息日用药熏消毒法对教室进行消毒,消毒过程中,室内每立方米空气中的含药量y(mg)与消毒开始后的时间x(h)之间的函数图象如图所示,其中药物释放完毕前y与x成正比例;药物释放完毕后,y与x成反比例.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
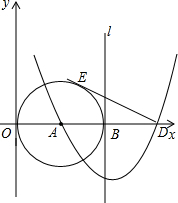 如图,已知点A(4,0),以A为圆心作⊙A与y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.
如图,已知点A(4,0),以A为圆心作⊙A与y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com