
【题目】某机构对2016年微信用户的职业颁布进行了随机抽样调查(职业说明:A:党政机关、军队,B:事业单位,C:企业,D:自由职业及人体户,E:学生,F:其他),图1和图2是根据调查数据绘制而成的不完整的统计图.请根据图中提供的信息,解答下列问题: 
(1)该机构共抽查微信用户人;
(2)在图1中,补全条形统计图;
(3)在图2中,“D”用户所对应扇形的圆心角度数为度;
(4)2016年微信用户约有7.5亿人,估计“E”用户大约有亿人.
【答案】
(1)50000
(2)解:如图;

(3)90
(4)1.08
【解析】解:(1)该机构共抽查微信用户1300÷2.6%=50000 人;(2)”C”用户人数为:50000×40%=20000人,(3)“D”用户所对应扇形的圆心角度数为 ![]() ;(4)2016年微信用户约有7.5亿人,估计“E”用户大约有7.5×
;(4)2016年微信用户约有7.5亿人,估计“E”用户大约有7.5× ![]() =1.08亿,
=1.08亿,
答:2016年微信用户约有7.5亿人,估计“E”用户大约有1.08亿人.
所以答案是:50000,90,1.08.

【考点精析】本题主要考查了扇形统计图和条形统计图的相关知识点,需要掌握能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】【发现】:如图1,在正三角形ABC中,在AB,AC边上分别取点M,N,BM=AN,连接BN,CM,相交于点O,求∠α
易得:△ABN≌△BCN,则∠1=∠2
∵∠α是△BOC的外角,∴∠α=∠2+∠3
∴∠α=∠1+∠3=∠ABC=60°
【推广】:在正n边形中,对相邻的两边实施同样的操作…
(1)如图2,在正四边形ABCD中,在AB,AD边上分别取点M,N,连接BN,CM,可确定∠α=°;
(2)如图3,在正五边形ABCDE中,在AB,AD边上分别取点M,N,连接BN,CM,可确定∠α=°;
(3)判断:∠α可以等于160°吗?如果可以,求出对应的边数n,若不可以,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
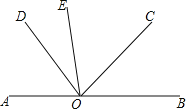
【题目】如图,已知,A、O、B在同一条直线上,∠AOE=∠COD,∠EOD=30°.
(1)若∠AOE=88°30′,求∠BOC的度数;
(2)若射线OC平分∠EOB,求∠BOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在6×6的正方形网格中,每个小正方形的边长为1,点A、B、C、D、E、F、M、N、P均为格点(格点是指每个小正方形的顶点).
(1)利用图①中的网格,过P点画直线MN的平行线和垂线.
(2)把图②网格中的三条线段AB、CD、EF通过平移使之首尾顺次相接组成一个三角形(在图②中画出三角形).
(3)第(2)小题中线段AB、CD、EF首尾顺次相接组成一个三角形的面积是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
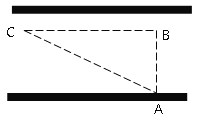
【题目】“道路交通管理条例”规定:小汽车在城街上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪A正前方30米B处,过了2秒后,测得小汽车C与车速检测仪A间距离为50米,这辆小汽车超速了吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD上一点,AB=8,BE=BC=10,动点P在线段BE上(与点B、E不重合),点Q在BC的延长线上,PE=CQ,PQ交EC于点F,PG∥BQ交EC于点G,设PE=x.
(1)求证:△PFG≌△QFC
(2)连结DG.当x为何值时,四边形PGDE是菱形,请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,D,E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,AC=5cm,则BD的长为( )
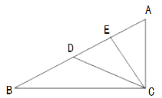
A. 5cm B. 6cm C. 7cm D. 8cm
查看答案和解析>>
科目:初中数学 来源: 题型:
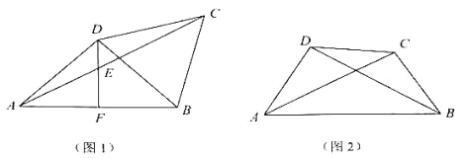
【题目】在四边形 ABCD 中,BC=CD,连接 AC、BD,∠ADB=90°.
(1)如图 1,若 AD=BD=BC,过点 D 作 DF⊥AB 于点 F,交 AC 于点 E:
①求∠DAC;
②猜想 AE、DE、CE 的数量关系,并证明你的猜想;
(2)如图 2,若 AC=BD,求∠DAC 的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com