
 如图,在平面直角坐标系中,AD平分∠OAB,DB⊥AB,BC∥OA,若点B的横坐标为1,点D的坐标为(0,$\sqrt{3}$),则点C的坐标是( )
如图,在平面直角坐标系中,AD平分∠OAB,DB⊥AB,BC∥OA,若点B的横坐标为1,点D的坐标为(0,$\sqrt{3}$),则点C的坐标是( )| A. | (0,2) | B. | (0,5) | C. | (0,$\sqrt{5}$) | D. | (0,$\sqrt{3}$+$\sqrt{2}$) |
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:选择题
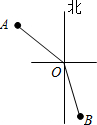 在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,则∠AOB的大小为( )
在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,则∠AOB的大小为( )| A. | 69° | B. | 111° | C. | 159° | D. | 141° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{5}$+$\sqrt{2}$=$\sqrt{7}$ | B. | $\sqrt{{a}^{2}-{b}^{2}}$=a-b | C. | $\sqrt{8}$-$\sqrt{18}$=-$\sqrt{2}$ | D. | $\frac{\sqrt{6}+\sqrt{8}}{2}$=$\sqrt{3}$+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 甲 | 乙 | 丙 | 丁 | |
| 平均数 | 70 | 86 | 86 | 79 |
| 方 差 | 6 | 7.5 | 7 | 7.5 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为( )
直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为( )| A. | x>-1 | B. | x<-2 | C. | x<-1 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
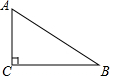 如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=4cm,若以点C为圆心,以2cm为半径作⊙C,则AB与⊙C的位置关系是( )
如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=4cm,若以点C为圆心,以2cm为半径作⊙C,则AB与⊙C的位置关系是( )| A. | 相离 | B. | 相切 | C. | 相交 | D. | 相切或相交 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,点D,E分别在AC,AB上且DE∥BC,若S△ADE:S△BDE=2:3,则S△ADE:S△ACB=( )
如图,在△ABC中,点D,E分别在AC,AB上且DE∥BC,若S△ADE:S△BDE=2:3,则S△ADE:S△ACB=( )| A. | 2:3 | B. | 4:9 | C. | 4:25 | D. | 4:19 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3(3x+2)-5x+1=12-6(2x-1) | B. | 3(3x+2)-5x-1=1-6(2x-1) | ||
| C. | 3(3x+2)-5x-1=12-6(2x-1) | D. | (3x+2)-5x+1=12-6(2x-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com