
ΓΨΧβΡΩΓΩΈ Χβ«ιΨΑΘΚ“ΜΫΎ ΐ―ßΩΈΚσΘ§άœ Π≤Φ÷ΟΝΥ“ΜΒάΝΖœΑΧβΘΚ
»γΆΦ1Θ§“―÷ΣRtΓςABC÷–Θ§ACΘΫBCΘ§ΓœABCΘΫ90ΓψΘ§CDΓΆAB”ΎΒψDΘ§ΒψEΘ§FΖ÷±π‘ΎADΚΆBC…œΘ§Γœ1ΘΫΓœ2Θ§FGΓΆAB”ΎΒψGΘ§«σ÷ΛΘΚΓςCDEΓ’ΓςEGF
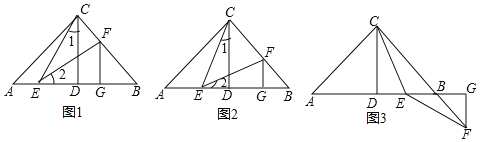
Θ®1Θ©‘ΡΕΝάμΫβΘ§Άξ≥…Ϋβ¥πΘΚ±ΨΧβ÷ΛΟςΒΡΥΦ¬ΖΩ…“‘”Οœ¬Ν–ΩρΆΦ±μ ΨΘΚ
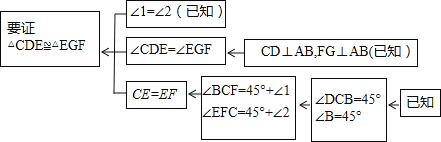
ΗυΨί…œ ωΥΦ¬ΖΘ§«κΡψΆξ’ϊΒΊ–¥≥ω’βΒάΝΖœΑΧβΒΡ÷ΛΟςΙΐ≥ΧΘΜ
Θ®2Θ©ΧΊ βΈΜ÷ΟΘ§÷ΛΟςΫα¬έΘΚ»γΆΦ2Θ§»τCEΤΫΖ÷ΓœACDΘ§Τδ”ύΧθΦΰ≤Μ±δΘ§≈–ΕœAEΚΆBFΒΡ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”…ΘΜ
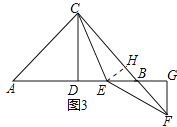
Θ®3Θ©÷Σ Ε«®“ΤΘ°ΧΫΨΩΖΔœ÷ΘΚ»γΆΦ3Θ§“―÷Σ‘ΎRtΓςABC÷–Θ§ACΘΫBCΘ§ΓœACBΘΫ90ΓψΘ§CDΓΆAB”ΎΒψDΘ§»τΒψE «DBΒΡ÷–ΒψΘ§ΒψF‘Ύ÷±œΏCB…œΘ§«“ECΘΫEFΘ§«κ÷±Ϋ”–¥≥ωBF”κAEΒΡ ΐΝΩΙΊœΒΘ°Θ®≤Μ±Ί–¥Ϋβ¥πΙΐ≥ΧΘ©
ΓΨ¥πΑΗΓΩΘ®1Θ©ΦϊΫβΈωΘΜΘ®2Θ©AEΘΫBFΘΜάμ”…ΦϊΫβΈωΘΜΘ®3Θ©AEΘΫ![]() BFΘ°
BFΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©œ»÷ΛΟςCEΘΫEFΘ§άϊ”ΟAASΕ®άμ÷ΛΟςΓςCDEΓ’ΓςEGFΘ®AASΘ©Φ¥Ω…ΘΜ
Θ®2Θ©œ»÷ΛΓœACEΘΫΓœ2Θ§‘Ό÷ΛΟςΓςACEΓ’ΓςBEFΘ®AASΘ©Θ§Φ¥Ω…ΒΟ÷ΛAEΘΫBFΘΜ
Θ®3Θ©ΉςEHΓΆBC”κHΘ§…ηDEΘΫxΘ§«σ≥ωAEΘΫ3xΘ§‘Ό÷Λ≥ωBFΘΫ![]() xΘ§Φ¥Ω…ΒΟ≥ωΫα¬έΘ°
xΘ§Φ¥Ω…ΒΟ≥ωΫα¬έΘ°
Θ®1Θ©÷ΛΟςΘΚΓΏACΘΫBCΘ§ΓœACBΘΫ90ΓψΘ§
ΓύΓœAΘΫΓœBΘΫ45ΓψΘ§
ÿCDâABȧ
ΓύΓœCDBΘΫ90ΓψΘ§
ΓύΓœDCBΘΫ45ΓψΘ§
ΓΏΓœECFΘΫΓœDCB+Γœ1ΘΫ45Γψ+Γœ1Θ§ΓœEFCΘΫΓœB+Γœ2ΘΫ45Γψ+Γœ2Θ§Γœ1ΘΫΓœ2Θ§
ΓύΓœECFΘΫΓœEFCΘ§
ΓύCEΘΫEFΘ§
ÿCDâABȧFGâABȧ
ΓύΓœCDEΘΫΓœEGFΘΫ90ΓψΘ§
‘ΎΓςCDEΚΆΓςEGF÷–Θ§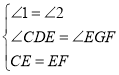 Θ§
Θ§
ΓύΓςCDEΓ’ΓςEGFΘ®AASΘ©ΘΜ
Θ®2Θ©÷ΛΟςΘΚ”…Θ®1Θ©ΒΟΘΚCEΘΫEFΘ§ΓœAΘΫΓœBΘ§
ΓΏCEΤΫΖ÷ΓœACDΘ§
ΓύΓœACEΘΫΓœ1Θ§
ΓΏΓœ1ΘΫΓœ2Θ§
ΓύΓœACEΘΫΓœ2Θ§
‘ΎΓςACEΚΆΓςBEF÷–Θ§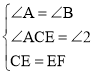 Θ§
Θ§
ΓύΓςACEΓ’ΓςBEFΘ®AASΘ©Θ§
ΓύAEΘΫBFΘΜ
Θ®3Θ©ΫβΘΚAEΘΫ![]() BFΘ§ΉςEHΓΆBC”κHΘ§»γΆΦ3Υυ ΨΘΚ
BFΘ§ΉςEHΓΆBC”κHΘ§»γΆΦ3Υυ ΨΘΚ
…ηDEΘΫxΘ§ΗυΨίΧβ“βΒΟΘΚBEΘΫDEΘΫxΘ§ADΘΫBDΘΫ2xΘ§CDΘΫADΘΫ2xΘ§AEΘΫ3xΘ§
ΗυΨίΙ¥Ι…Ε®άμΒΟΘΚBCΘΫACΘΫ2![]() xΘ§
xȧ
ΓΏΓœABCΘΫ45ΓψΘ§EHΓΆBCΘ§
ΓύBHΘΫ![]() xΘ§
xȧ
ΓύCHΘΫBC©¹BHΘΫ![]() xΘ§
xȧ
ΓΏECΘΫEFΘ§
ΓύFHΘΫCHΘΫ![]() xΘ§
xȧ
ΓύBFΘΫ![]() x©¹
x©¹![]() xΘΫ
xΘΫ![]() xΘ§
xȧ
Γύ![]() ΘΫ
ΘΫ![]() ΘΫ
ΘΫ![]() Θ§
Θ§
ΓύAEΘΫ![]() BFΘ°
BFΘ°


 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥―ß–Θ≥θΕΰΚΆ≥θ»ΐΝΫΗωΡξΦΕΗς”–600ΟϊΆ§―ßΘ§ΈΣΝΥΩΤΤ’Έά…ζΖά“Ώ÷Σ ΕΘ§―ß–ΘΉι÷·ΝΥ“Μ¥Έ‘ΎœΏ÷Σ ΕΨΚ»ϋΘ§–Γ”νΖ÷±π¥”≥θΕΰΓΔ≥θ»ΐΝΫΗωΡξΦΕΥφΜζ≥ι»ΓΝΥ40ΟϊΆ§―ßΒΡ≥…Φ®Θ®ΑΌΖ÷÷ΤΘ©Θ§≤ΔΕ‘ ΐΨίΘ®≥…Φ®Θ©Ϋχ––’ϊάμΓΔΟη ωΚΆΖ÷ΈωΘ§œ¬ΟφΗχ≥ωΝΥ≤ΩΖ÷–≈œΔΘ°
![]() Θ°≥θΕΰΓΔ≥θ»ΐΡξΦΕ―ß…ζ÷Σ ΕΨΚ»ϋ≥…Φ®≤ΜΆξ’ϊΒΡΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦ»γœ¬Θ® ΐΨίΖ÷≥…5ΉιΘΚ
Θ°≥θΕΰΓΔ≥θ»ΐΡξΦΕ―ß…ζ÷Σ ΕΨΚ»ϋ≥…Φ®≤ΜΆξ’ϊΒΡΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦ»γœ¬Θ® ΐΨίΖ÷≥…5ΉιΘΚ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ©ΘΚ
Θ©ΘΚ
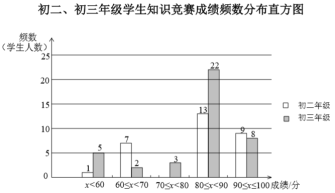
![]() Θ°≥θΕΰΡξΦΕ―ß…ζ÷Σ ΕΨΚ»ϋ≥…Φ®‘Ύ
Θ°≥θΕΰΡξΦΕ―ß…ζ÷Σ ΕΨΚ»ϋ≥…Φ®‘Ύ![]() ’β“ΜΉιΒΡ ΐΨί»γœ¬ΘΚ
’β“ΜΉιΒΡ ΐΨί»γœ¬ΘΚ
80 80 81 83 83 84 84 85 86 87 88 89 89
![]() Θ°≥θΕΰΓΔ≥θ»ΐ―ß…ζ÷Σ ΕΨΚ»ϋ≥…Φ®ΒΡΤΫΨυ ΐΓΔ÷–ΈΜ ΐΓΔΖΫ≤ν»γœ¬ΘΚ
Θ°≥θΕΰΓΔ≥θ»ΐ―ß…ζ÷Σ ΕΨΚ»ϋ≥…Φ®ΒΡΤΫΨυ ΐΓΔ÷–ΈΜ ΐΓΔΖΫ≤ν»γœ¬ΘΚ
ΤΫΨυ ΐ | ÷–ΈΜ ΐ | ΖΫ≤ν | |
≥θΕΰΡξΦΕ | 80.8 |
| 96.9 |
≥θ»ΐΡξΦΕ | 80.6 | 86 | 153.3 |
ΗυΨί“‘…œ–≈œΔΘ§ΜΊ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©≤Ι»Ϊ…œΟφΒΡ÷Σ ΕΨΚ»ϋ≥…Φ®ΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦΘΜ
Θ®2Θ©–¥≥ω±μ÷–![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®3Θ©![]() Ά§―ßΩ¥ΒΫ…œ ωΒΡ–≈œΔΚσΘ§ΥΒΉ‘ΦΚΒΡ≥…Φ®Ρή‘Ύ±ΨΡξΦΕ≈≈‘Ύ«Α40%Θ§
Ά§―ßΩ¥ΒΫ…œ ωΒΡ–≈œΔΚσΘ§ΥΒΉ‘ΦΚΒΡ≥…Φ®Ρή‘Ύ±ΨΡξΦΕ≈≈‘Ύ«Α40%Θ§![]() Ά§―ßΩ¥ΒΫ
Ά§―ßΩ¥ΒΫ![]() Ά§―ßΒΡ≥…Φ®ΚσΥΒΘΚΓΑΚή“≈ΚΕΘ§ΡψΒΡ≥…Φ®‘ΎΈ“Ο«ΡξΦΕΫχ≤ΜΝΥ«Α50%Γ±Θ°«κ≈–Εœ
Ά§―ßΒΡ≥…Φ®ΚσΥΒΘΚΓΑΚή“≈ΚΕΘ§ΡψΒΡ≥…Φ®‘ΎΈ“Ο«ΡξΦΕΫχ≤ΜΝΥ«Α50%Γ±Θ°«κ≈–Εœ![]() Ά§―ß «________Θ®ΧνΓΑ≥θΕΰΓ±ΜρΓΑ≥θ»ΐΓ±Θ©ΡξΦΕΒΡ―ßΘ§Ρψ≈–ΕœΒΡάμ”… «________Θ°
Ά§―ß «________Θ®ΧνΓΑ≥θΕΰΓ±ΜρΓΑ≥θ»ΐΓ±Θ©ΡξΦΕΒΡ―ßΘ§Ρψ≈–ΕœΒΡάμ”… «________Θ°
Θ®4Θ©»τ≥…Φ®‘Ύ85Ζ÷ΦΑ“‘…œΈΣ”≈–ψΘ§«κΙάΦΤ≥θΕΰΡξΦΕΨΚ»ϋ≥…Φ®”≈–ψΒΡ»Υ ΐΈΣ____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ¥”©¹4ΓΔ3ΓΔ5’β»ΐΗω ΐ÷–Θ§ΥφΜζ≥ι»Γ“ΜΗω ΐΘ§Φ«ΈΣaΘ§Ρ«Ο¥Θ§ ΙΙΊ”ΎxΒΡΖΫ≥Χx2+4x+aΘΫ0”–ΫβΘ§«“ ΙΙΊ”ΎxΒΡ“Μ¥ΈΚ· ΐyΘΫ2x+aΒΡΆΦœσ”κx÷αΓΔy÷αΈß≥…ΒΡ»ΐΫ«–ΈΟφΜΐ«ΓΚΟΈΣ4ΒΡΗ≈¬ _____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®6Ζ÷Θ©Ρ≥ΚΘ”ρ”–AΘ§BΝΫΗωΗέΩΎΘ§BΗέΩΎ‘ΎAΗέΩΎ±±ΤΪΈς30ΓψΖΫœρ…œΘ§ΨύAΗέΩΎ60ΚΘάοΘ§”–“ΜΥ“¥§¥”AΗέΩΎ≥ωΖΔΘ§―ΊΕΪ±±ΖΫœρ–– Μ“ΜΕΈΨύάκΚσΘ§ΒΫ¥οΈΜ”ΎBΗέΩΎΡœΤΪΕΪ75ΓψΖΫœρΒΡC¥ΠΘ§«σΗΟ¥§”κBΗέΩΎ÷°ΦδΒΡΨύάκΦ¥CBΒΡ≥ΛΘ®ΫαΙϊ±ΘΝτΗυΚ≈Θ©Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§Νβ–ΈOABCΒΡΕΞΒψA‘Ύx÷α…œΘ§ΕΞΒψBΒΡΉχ±ξΈΣΘ®8Θ§4Θ©Θ§ΒψP «Ε‘Ϋ«œΏOB…œ“ΜΗωΕ·ΒψΘ§ΒψDΒΡΉχ±ξΈΣΘ®0Θ§©¹2Θ©Θ§Β±DP”κAP÷°ΚΆΉν–Γ ±Θ§ΒψPΒΡΉχ±ξΈΣ_____Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΓςABC «Β»±Ώ»ΐΫ«–ΈΘ§ΒψDΓΔEΖ÷±π‘Ύ±ΏBCΓΔAC…œΘ§«“CD=CEΘ§Ν§Ϋ”DE≤Δ―”≥Λ÷ΝΒψFΘ§ ΙEF=AEΘ§Ν§Ϋ”AFΘ§CFΘ§Ν§Ϋ”BE≤Δ―”≥ΛΫΜCF”ΎΒψGΘ°œ¬Ν–Ϋα¬έΘΚ
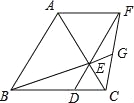
ΔΌΓςABEΓ’ΓςACFΘΜΔΎBC=DFΘΜΔέSΓςABC=SΓςACF+SΓςDCFΘΜΔή»τBD=2DCΘ§‘ρGF=2EGΘ°Τδ÷–’ΐ»ΖΒΡΫα¬έ « Θ°Θ®Χν–¥Υυ”–’ΐ»ΖΫα¬έΒΡ–ρΚ≈Θ©
ΓΨ¥πΑΗΓΩΔΌΔΎΔέΔή.
ΓΨΫβΈωΓΩ
‘ΧβΖ÷ΈωΘΚΔΌ”…ΓςABC «Β»±Ώ»ΐΫ«–ΈΘ§Ω…ΒΟAB=AC=BCΘ§ΓœBAC=ΓœACB=60ΓψΘ§‘Ό“ρDE=DCΘ§Ω…≈–Ε®ΓςDEC «Β»±Ώ»ΐΫ«–ΈΘ§Υυ“‘ED=EC=DCΘ§ΓœDEC=ΓœAEF=60ΓψΘ§
“ρEF=AEΘ§Υυ“‘ΓςAEF «Β»±Ώ»ΐΫ«–ΈΘ§Υυ“‘AF=AEΘ§ΓœEAF=60ΓψΘ§‘ΎΓςABEΚΆΓςACF÷–Θ§AB=AC,ΓœBAE=ΓœCAF,AE=AF Θ§Ω…≈–Ε®ΓςABEΓ’ΓςACFΘ§Ι ΔΌ’ΐ»ΖΘ°ΔΎ”…ΓœABC=ΓœFDCΘ§Ω…ΒΟABΓΈDFΘ§‘Ό“ρΓœEAF=ΓœACB=60ΓψΘ§Ω…ΒΟABΓΈAFΘ§Φ¥Ω…≈–Ε®ΥΡ±Ώ–ΈABDF «ΤΫ––ΥΡ±Ώ–ΈΘ§Υυ“‘DF=AB=BCΘ§Ι ΔΎ’ΐ»ΖΘ°Δέ”…ΓςABEΓ’ΓςACFΩ…ΒΟBE=CFΘ§SΓςABE=SΓςAFCΘ§‘ΎΓςBCEΚΆΓςFDC÷–Θ§BC=DF,CE=CD,BE=CF Θ§Ω…≈–Ε®ΓςBCEΓ’ΓςFDCΘ§Υυ“‘SΓςBCE=SΓςFDCΘ§Φ¥Ω…ΒΟSΓςABC=SΓςABE+SΓςBCE=SΓςACF+SΓςBCE=SΓςABC=SΓςACF+SΓςDCFΘ§Ι Δέ’ΐ»ΖΘ°Δή”…ΓςBCEΓ’ΓςFDCΘ§Ω…ΒΟΓœDBE=ΓœEFGΘ§‘Ό”…ΓœBED=ΓœFEGΩ…≈–Ε®ΓςBDEΓΉΓςFGEΘ§Υυ“‘![]() =
=![]() Θ§Φ¥
Θ§Φ¥![]() =
=![]() Θ§”÷“ρBD=2DCΘ§DC=DEΘ§Ω…ΒΟ
Θ§”÷“ρBD=2DCΘ§DC=DEΘ§Ω…ΒΟ![]() =2Θ§Φ¥FG=2EGΘ°Ι Δή’ΐ»ΖΘ°
=2Θ§Φ¥FG=2EGΘ°Ι Δή’ΐ»ΖΘ°
ΩΦΒψΘΚ»ΐΫ«–ΈΉέΚœΧβ.
ΓΨΧβ–ΆΓΩΧνΩ’Χβ
ΓΨΫα χΓΩ
19
ΓΨΧβΡΩΓΩœ»Μ·ΦρΘ§‘Ό«σ÷ΒΘΚ(aΘΪ1Θ≠![]() )Γ¬(
)Γ¬(![]() )Θ§Τδ÷–aΘΫ2ΘΪ
)Θ§Τδ÷–aΘΫ2ΘΪ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ ήΖ«÷ό÷μΈΝ“Ώ«ι”ΑœλΘ§2019ΡξΈ“Ιζ÷μ»βΦέΗώ”–Ϋœ¥σΖυΕ»ΒΡ…œ…ΐΘ°ΈΣΝΥΫβΡ≥ΒΊ«χ―χ÷≥ΜßΒΡ ή‘÷«ιΩωΘ§œ÷¥”ΗΟΒΊ«χΫ®ΒΒΒΡ―χ÷≥Μß÷–ΥφΜζ≥ι»ΓΝΥ≤ΩΖ÷―χ÷≥ΜßΫχ––Βς≤ιΘ®Α―Βς≤ιΫαΙϊΖ÷ΈΣΥΡΗωΒ»ΦΕΘΚAΦΕ-Ζ«≥Θ―œ÷ΊΘ§BΦΕ-―œ÷ΊΘ§CΦΕ-“ΜΑψΘ§DΦΕ-ΟΜ”–Η–»ΨΘ©Θ§≤ΔΫΪΒς≤ιΫαΙϊΜφ÷Τ≥…»γœ¬ΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘ°«κΗυΨίΆ≥ΦΤΆΦ÷–ΒΡ–≈œΔΫβ¥πœ¬Ν–Έ ΧβΘΚ
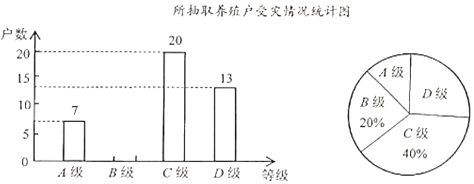
Θ®1Θ©ΧνΩ’ΘΚ±Ψ¥Έ≥ι―υΒς≤ιΒΡ―χ÷≥ΜßΒΡΉήΜß ΐ «______ΘΜ‘Ύ…»–ΈΆ≥ΦΤΆΦ÷–![]() ΦΕΥυΕ‘”ΠΒΡ‘≤–ΡΫ«ΈΣ______Ε»ΘΜ
ΦΕΥυΕ‘”ΠΒΡ‘≤–ΡΫ«ΈΣ______Ε»ΘΜ
Θ®2Θ©«κ≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΘΜ
Θ®3Θ©»τΗΟΒΊ«χΫ®ΒΒΒΡ―χ÷≥Μß”–1500ΜßΘ§ΙάΦΤΖ«≥Θ―œ÷Ί”κ―œ÷ΊΒΡ―χ÷≥Μß“ΜΙ≤”–Εύ…ΌΜßΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
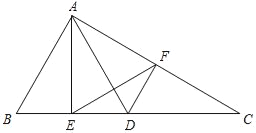
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§ΒψDΈΣ±ΏBC…œ“ΜΒψΘ§«“ADΘΫABΘ§AEΓΆBCΘ§¥ΙΉψΈΣΒψEΘ°ΙΐΒψDΉςDFΓΈABΘ§ΫΜ±ΏAC”ΎΒψFΘ§Ν§Ϋ”EFΘ§EF2ΘΫ![]() BDECΘ°
BDECΘ°
(1)«σ÷ΛΘΚΓςEDFΓΉΓςEFCΘΜ
(2)»γΙϊ![]() Θ§«σ÷ΛΘΚABΘΫBDΘ°
Θ§«σ÷ΛΘΚABΘΫBDΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
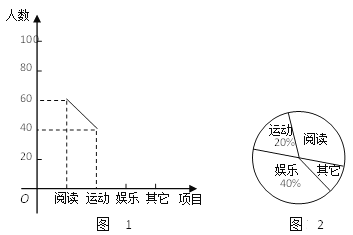
ΓΨΧβΡΩΓΩΡ≥÷–―ßΆ≈Έ·ΜαΈΣ―–ΨΩΗΟ–Θ―ß…ζΒΡΩΈ”ύΜνΕ·«ιΩωΘ§≤…»Γ≥ι―υΒΡΖΫΖ®Θ§¥”‘ΡΕΝΓΔ‘ΥΕ·ΓΔ”ιά÷ΓΔΤδΥϋΒ»ΥΡΗωΖΫΟφΒς≤ιΝΥ»τΗ…Οϊ―ß…ζΒΡ–Υ»ΛΑ°ΚΟΘ§≤ΔΫΪΒς≤ιΒΡΫαΙϊΜφ÷ΤΝΥ»γœ¬ΒΡΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘ®»γΆΦ1Θ§ΆΦ2Θ©Θ§«κΡψΗυΨίΆΦ÷–ΧαΙ©ΒΡ–≈œΔΫβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©‘Ύ’β¥Έ―–ΨΩ÷–Θ§“ΜΙ≤Βς≤ιΝΥΕύ…ΌΟϊ―ß…ζΘΩ
Θ®2Θ©ΓΑΤδΥϋΓ±‘Ύ…»–ΈΆΦ÷–Υυ’ΦΒΡ‘≤–ΡΫ« «Εύ…ΌΕ»ΘΩ
Θ®3Θ©≤Ι»ΪΤΒ ΐΖ÷≤Φ’έœΏΆΦΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com