
分析 设学校到甲班下车的地方的距离是x千米,根据乙组步行的时间等于车子从出发到与乙相遇的时间列一元一次方程解答.
解答 解:设学校到甲班下车的地方的距离是x千米,甲乙二组步行的距离是(27-x)千米,
根据乙组步行的时间等于车子从出发到与乙相遇的时间,列方程得,
$\frac{27-x}{4}$=$\frac{x+[27-2(27-x)]}{60}$
解得:x=24(千米),
27-x=3(千米),
所行的时间是:$\frac{3}{4}$+$\frac{24}{60}$=1.15小时=1小时9分,
8小时+1小时9分钟=9时9分,
答:两个班最早9时9分同时到.
点评 本题主要考查了一元一次方程的实际应用,熟练的运用速度、时间、路程之间的数量关系找到等量关系是解决问题的关键.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
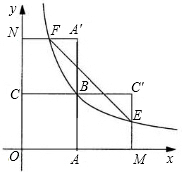 如图,四边形OABC是面积为4的正方形,双曲线经过点B.
如图,四边形OABC是面积为4的正方形,双曲线经过点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 据媒体报道,近期“甲型H7N9禽流感”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“甲型H7N9禽流感”,对教室进行“熏药消毒”.已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示,第一段是线段OA,第二段是一个反比例函数的图象(即图中A点及其右侧的部分),根据图象所示信息,解答下列问题:
据媒体报道,近期“甲型H7N9禽流感”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“甲型H7N9禽流感”,对教室进行“熏药消毒”.已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示,第一段是线段OA,第二段是一个反比例函数的图象(即图中A点及其右侧的部分),根据图象所示信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
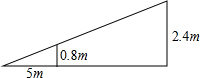 如图,小芳在达网球时,为使球恰好能过网(网高0.8米),且落在对方区域内离网5米的位置上,如果她的击球高度是2.4米,则应站在离网的( )
如图,小芳在达网球时,为使球恰好能过网(网高0.8米),且落在对方区域内离网5米的位置上,如果她的击球高度是2.4米,则应站在离网的( )| A. | 15米处 | B. | 10米处 | C. | 8米处 | D. | 7.5米处 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB是⊙O的直径,它与弦CD交于点E.我们给出下列结论:
如图,AB是⊙O的直径,它与弦CD交于点E.我们给出下列结论:| A. | ①②③④ | B. | ①②③ | C. | ②③ | D. | ②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com