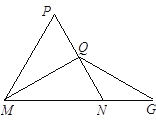
[题目]如下图.△MNP中.∠P=60°.MN=NP.MQ⊥PN.垂足为Q.延长MN至G.取NG=NQ.若△MNP的周长为12.MQ=a.则△MGQ周长是( )A. 8+2a B. 8+a C. 6+a D. 6+2a 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如下图，△MNP中，∠P=60°，MN=NP，MQ⊥PN，垂足为Q，延长MN至G，取NG=NQ，若△MNP的周长为12，MQ=a，则△MGQ周长是（）

A. 8+2a B. 8+a C. 6+a D. 6+2a

【答案】D

【解析】

试题由∠P=60°，MN=NP，可得△MNP是等边三角形，再根据等边三角形的“三线合一”的性质以及等腰三角形的判定，即可求得结果。

∵∠P=60°，MN=NP

∴△MNP是等边三角形．

又∵MQ⊥PN，垂足为Q，

∴PM=PN=MN=4，NQ=NG=2，MQ=a，∠QMN=30°，∠PNM=60°，

∵NG=NQ，

∴∠G=∠QMN，

∴QG=MQ=a，

∵△MNP的周长为12，

∴MN=4，NG=2，

∴△MGQ周长是6+2a．

故选D．

练习册系列答案

暑假生活湖南少年儿童出版社系列答案

暑假小小练系列答案

暑假作业新世界出版社系列答案

创新成功学习快乐暑假云南科技出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

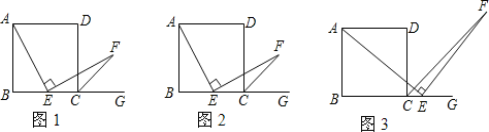
【题目】数学课上,张老师出示了问题：如图1,四边形ABCD是正方形,点E是边BC的中点.∠AEF=90°，且EF交正方形外角∠DCG的平分线CF于点F，求证：AE=EF.

经过思考,小明展示了一种正确的解题思路：在AB上截取BM=BE,连接ME，则AM=EC,易证△AME≌△ECF，所以AE=EF.

在此基础上，同学们作了进一步的研究：

(1)小颖提出：如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”，其它条件不变，那么结论“AE=EF”仍然成立，你认为小颖的观点正确吗?如果正确，写出证明过程；如果不正确，请说明理由；

(2)小华提出：如图3,点E是BC的延长线上(除C点外)的任意一点，其他条件不变，结论“AE=EF”仍然成立。你认为小华的观点正确吗?如果正确，写出证明过程；如果不正确，请说明理由。

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图所示，△ABC的三个顶点的坐标为A（1,0），B（6,0），C（3，-4）.

（1）求△ABC的面积

（2）若A，B两点的位置不变，点P在轴什么位置时，的面积是面积的2倍；

（3）若A，B两点的位置不变，点P在轴什么位置时，的面积是面积的2倍；

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某超市为庆祝开业举办大酬宾抽奖活动，凡在开业当天进店购物的顾客，都能获得一次抽奖的机会，抽奖规则如下：在一个不透明的盒子里装有分别标有数字1、2、3、4的4个小球，它们的形状、大小、质地完全相同，顾客先从盒子里随机取出一个小球，记下小球上标有的数字，然后把小球放回盒子并搅拌均匀，再从盒子中随机取出一个小球，记下小球上标有的数字，并计算两次记下的数字之和，若两次所得的数字之和为8，则可获得50元代金券一张；若所得的数字之和为6，则可获得30元代金券一张；若所得的数字之和为5，则可获得15元代金券一张；其他情况都不中奖．
（1）请用列表或树状图（树状图也称树形图）的方法（选其中一种即可），把抽奖一次可能出现的结果表示出来；
（2）假如你参加了该超市开业当天的一次抽奖活动，求能中奖的概率P．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在Rt△ABC中，（M2，N2），∠BAC=30°，E为AB边的中点，以BE为边作等边△BDE，连接AD，CD．

（1）求证：△ADE≌△CDB；

（2）若BC=，在AC边上找一点H，使得BH+EH最小，并求出这个最小值．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，等腰Rt△ABC中，∠ACB=90°，AC=BC=1，且AC边在直线a上，将△ABC绕点A顺时针旋转到位置①可得到点P1 ，此时AP1= ；将位置①的三角形绕点P1顺时针旋转到位置②可得到点P2 ，此时AP2= +1；将位置②的三角形绕点P2顺时针旋转到位置③可得到点P3时，AP3= +2…按此规律继续旋转，直至得到点P2026为止，则AP2016= ．