
【题目】如图,在平行四边形ABCD中,AE平分∠DAB,已知CE=6,BE=8,DE=10.
(1)求BC的长;
(2)若∠CBE=36°,求∠ADC.
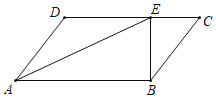
【答案】(1)BC=10;(2)126°.
【解析】
(1)依据DC∥AB,可得∠DEA=∠EAB,依据AE平分∠DAB,可得∠DAE=∠EAB,再根据∠DAE=∠DEA,即可得到AD=DE=10,进而得出BC=10;
(2)依据勾股定理的逆定理即可得出∠BEC=90°,再根据三角形内角和定理得出∠C的度数,进而得到∠ADC的度数.
解:(1)∵四边形ABCD是平行四边形,
∴AD=BC,DC∥AB,
∴∠DEA=∠EAB,
∵AE平分∠DAB,
∴∠DAE=∠EAB,
∴∠DAE=∠DEA,
∴AD=DE=10,
∴BC=10;
(2)∵CE=6,BE=8,BC=10,
∴CE2+BE2=62+82=100=BC2,
∴△BCE是直角三角形,且∠BEC=90°,
∴∠C=90°﹣∠CBE=90°﹣36°=54°,
∵AD∥BC,
∴∠D=180°﹣∠C=180°﹣54°=126°.


科目:初中数学 来源: 题型:
【题目】如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M、N分别是DC、DF的中点,连接MN.若AB=7,BE=5,则MN=_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以边长为4![]() +4的等边三角形AOB的顶点O为坐标原点,边OA所在直线为x轴建立平面直角坐标系,点B在第一象限,在边OB上有一点P为OB的黄金分割点(PO>PB),那么点P的坐标是__.
+4的等边三角形AOB的顶点O为坐标原点,边OA所在直线为x轴建立平面直角坐标系,点B在第一象限,在边OB上有一点P为OB的黄金分割点(PO>PB),那么点P的坐标是__.
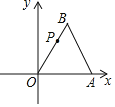
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB表达式为y=﹣2x+2,交x轴于点A,交y轴于点B.若y轴负半轴上有一点C,且CO=![]() AO.
AO.
(1)求点C的坐标和直线AC的表达式;
(2)在直线AC上是否存在点D,使以点A、B、D为顶点的三角形与△ABO相似?若存在,请求出点D的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:![]() .
.
(2)若AB=12,BM=5,求DE的长.
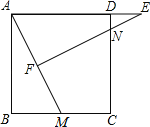
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E是BC的中点,连接DE,过点A作AG⊥ED交DE于点F,交CD于点G.
(1)若BC=4,求AG的长;
(2)连接BF,求证:AB=FB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为践行“绿水青山就是金山银山”的理念,及时推广生态文明建设,某校组织全校师生参与植树节活动.为调査栽种的柳树的成活情况,对全校学生的植树情况进行了抽样调查,并将调查结果分为“A.优良”“B.合格”C.差”三类.
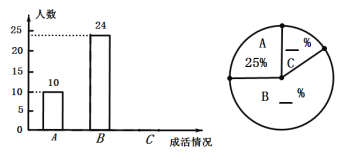
请根据图中信息,解答下列问题.
(1)求被调查学生的人数.
(2)将上面的条形统计图与扇形统计图补充完整.
(3)已知植树小组“勤奋组”的4名学生所种的四棵树中(每棵树对应一名责任人),A类1棵,B类2棵,C类1棵,该小组恰好有两棵树被抽査,求恰好是两棵B类树被抽查的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B

(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6![]() ,AF=4
,AF=4![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最小值和最大值之和是( )
,点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最小值和最大值之和是( )
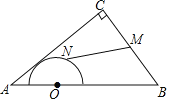
A. 5B. 6C. 7D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com