
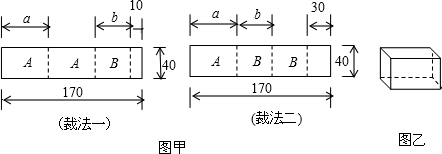
分析 (1)由图示利用板材的长列出关于a、b的二元一次方程组求解;
(2)①根据已知和图示计算出两种裁法共产生A型板材和B型板材的张数;
②根据竖式与横式礼品盒所需要的A、B两种型号板材的张数列出关于x、y的二元一次方程组,然后求解即可.
解答 解:由题意得:$\left\{\begin{array}{l}{2a+b+10=170}\\{a+2b+30=170}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=60}\\{b=40}\end{array}\right.$;
(2)①由图示裁法一产生A型板材为:2×m=2m,裁法二产生A型板材为:1×n=n,
所以两种裁法共产生A型板材为2m+n(张),
由图示裁法一产生B型板材为:1×m=m,裁法二产生A型板材为,2×n=2n,
所以两种裁法共产生B型板材为(m+2n)张;
故答案为:2m+n;m+2n;24或27或30.
点评 本题考查的知识点是二元一次方程组的应用,关键是正确理解题意,找出题目中的等量关系,列出方程组.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 时间(小时) | 7 | 8 | 9 | 10 |
| 人数(人) | 3 | 17 | 14 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{x}$ | C. | $\frac{x+1}{x}$ | D. | $\frac{x-1}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
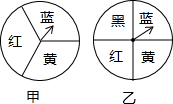 如图,有甲、乙两个转盘,每个转盘上各个扇形的圆心角都相等,让两个转盘分别自由转动一次,当转盘指针落在分界线上时,重新转动.
如图,有甲、乙两个转盘,每个转盘上各个扇形的圆心角都相等,让两个转盘分别自由转动一次,当转盘指针落在分界线上时,重新转动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com