
分析 (1)直接利用等边三角形的判定与性质得出答案;
(2)利用旋转的性质得出对应线段的关系,进而得出△AEF是等边三角形,得出答案即可;
(3)利用轴对称的性质得出画点P关于边AB的对称点G,画点P关于边AC的对称点H,进而得出△AGH是等边三角形,进而得出答案.
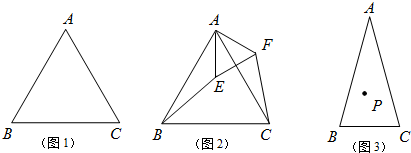
解答 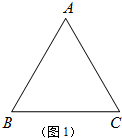 解:(1)如图1,∵AB=AC,∠B=60°,
解:(1)如图1,∵AB=AC,∠B=60°,
∴△ABC是等边三角形,
∴△ABC共有3条对称轴,∠A=60°,∠C=60°,
故答案为:3,60,60;
(2)如图2,∵AB=AC,∠ABC=60°
∴△ABC是等边三角形,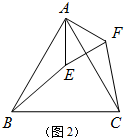
∴∠BAC=∠ABC=60°,
∵△ACF是由△ABE绕点A旋转而得到的,且边AB与AC重合
∴∠EAF=∠BAC=60°,AF=AE,
∴△AEF是等边三角形,
∴EF=AE=3;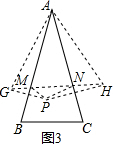 (3)如图3,画图方法:
(3)如图3,画图方法:
①画点P关于边AB的对称点G,
②画点P关于边AC的对称点H,
③连结GH,分别交AB、AC于点M、N,
此时△PMN周长最小.△PMN周长最小值为2.
点评 此题主要考查了旋转变换以及等边三角形的判定与性质,正确应用等边三角形的判定与性质是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{9}$=±3 | B. | $\sqrt{5}$-$\sqrt{4}$=1 | C. | $\sqrt{(3-π)^{2}}$=3-π | D. | $\root{3}{{2}^{3}}$=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 杀伤半径 | 20≤x<40 | 40≤x<60 | 60≤x<80 | 80≤x<100 |
| 数量 | 8 | 12 | 25 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com