
【题目】如图(1),平面直角坐标系中,一次函数y=﹣x+1的图象与y轴交于点A,点B是第二象限一次函数y=﹣x+1的图象上一点,且S△OAB=3,点C的坐标为(﹣2,﹣3).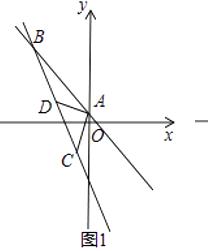
(1)求A,B的坐标;
(2)如图(1)若点D是线段BC上一点,且三角形ABD的面积是三角形ABC的一半,求△ABC的面积和点D的坐标;
(3)在(2)的条件下,如图(2),将线段AC沿直线AB平移,点A的对应点为A1 , 点C的对应点为C1 , 连接A1D,C1D,当△A1C1D直角三角形时,求A1的坐标.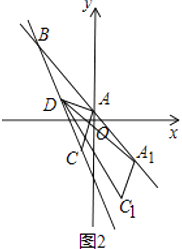
【答案】
(1)解:∵一次函数y=﹣x+1的图象与y轴交于点A,
∴当x=0时,y=1,
∴点A的坐标为(0,1),
∴OA=1
∵S△OAB=3,
∴ ![]() |xB|OA=3,
|xB|OA=3,
∴|xB|=6,
∵点B是第二象限一次函数y=﹣x+1的图象上一点,
∴B的横坐标为:﹣6,
则y=﹣(﹣6)+1=7,
∴点B的坐标为:(﹣6,7)
(2)解:如图1,过点B作BE⊥x轴,过点C作CF⊥y轴于点F,交BE于点E, 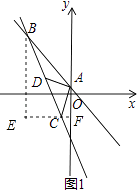
∵点C的坐标为(﹣2,﹣3),
∴BE=10,EF=6,EC=4,CF=2,AF=4,
∴S△ABC=S梯形ABEF﹣S△ACF﹣S△BEC= ![]() ×(4+10)×6﹣
×(4+10)×6﹣ ![]() ×4×2﹣
×4×2﹣ ![]() ×10×4=18;
×10×4=18;
∵点D是线段BC上一点,且三角形ABD的面积是三角形ABC的一半,
∴点D是BC的中点,
∴点D的坐标为:(﹣4,2)
(3)解:如图2,∵A(0,1),C(﹣2,﹣3),
∴由平移可知:点C是点A向左平移2个单位,再向下平移4个单位所得,
设A1(x,﹣x+1),则C1(x﹣2,﹣x+1﹣4),即(x﹣2,﹣x﹣3),
当△A1C1D直角三角形时,分三种情况:
①当∠DA1C1=90°时,如图2,由勾股定理得: ![]() =
= ![]() ,
,
∴(x+4)2+(﹣x+1﹣2)2+(x﹣2﹣x)2+(﹣x﹣3+x﹣1)2=(x﹣2+4)2+(﹣x﹣3﹣2)2
解得:x=2,
∴A1(2,﹣1);
②当∠A1C1D=90°时,如图3,由勾股定理得: ![]() ,
, 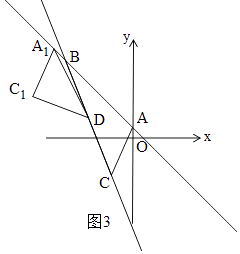
∴(x﹣2﹣x)2+(﹣x﹣3+x﹣1)2+(x﹣2+4)2+(﹣x﹣3﹣2)2=(x+4)2+(﹣x+1﹣2)2,
解得:x=﹣8,
∴A1(﹣8,9);
③当∠A1DC1=90°时,如图4和图5,由勾股定理得:A1D2+C1D2=A1C12,
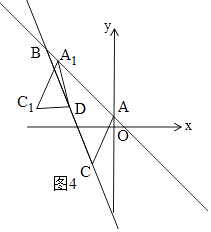
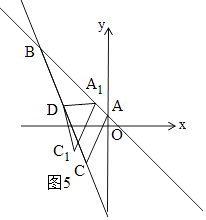
∴(x+4)2+(﹣x+1﹣2)2+(x﹣2+4)2+(﹣x﹣3﹣2)2=(x﹣2﹣x)2+(﹣x﹣3+x﹣1)2,
2x2+12x+13=0,
解得:x= ![]() ,
,
∴A1( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() );
);
综上所述,点A1的坐标为:(2,﹣1)或(﹣8,9)或( ![]() ,
, ![]()
![]() ,
, ![]() )
)
【解析】①一次函数y=﹣x+1的图象与y轴交于点A,求出点A的坐标为(0,1),点B是第二象限一次函数y=﹣x+1的图象上一点,得到B的横坐标为﹣6,求出点B的坐标为:(﹣6,7);②过点B作BE⊥x轴,过点C作CF⊥y轴于点F,交BE于点E,点C的坐标为(﹣2,﹣3),求出BE=10,EF=6,EC=4,CF=2,AF=4,S△ABC=S梯形ABEF﹣S△ACF﹣S△BEC=18,求出点D的坐标为:(﹣4,2);③由平移可知:点C是点A向左平移2个单位,再向下平移4个单位所得,当△A1C1D直角三角形时,分三种情况当∠DA1C1=90°时,如图2,由勾股定理得: A 1 D 2 + A 1 C 1 2 = D C 1 2 ,求出A1(2,﹣1);当∠A1C1D=90°时,由勾股定理得x=﹣8,得到A1(﹣8,9);当∠A1DC1=90°时,由勾股定理求出x的值,得到A1的坐标.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,锐角三角形ABC中,直线L为BC的中垂线,直线M为∠ABC的角平分线,L与M相交于P点.若∠A=60°,∠ACP=24°,则∠ABP的度数为何?( )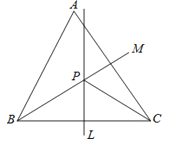
A.24°
B.30°
C.32°
D.36°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列表中的对应值:
x | 2.1 | 2.2 | 2.3 | 2.4 |
ax2+bx+c | ﹣1.39 | ﹣0.76 | ﹣0.11 | 0.56 |
判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副含![]() 和
和![]() 角的三角板
角的三角板![]() 和
和![]() 叠合在一起,边
叠合在一起,边![]() 与
与![]() 重合,
重合,![]() (如图1),点
(如图1),点![]() 为边
为边![]()
![]() 的中点,边
的中点,边![]() 与
与![]() 相交于点
相交于点![]() ,此时线段
,此时线段![]() 的长是 .现将三角板
的长是 .现将三角板![]() 绕点
绕点![]() 按顺时针方向旋转(如图2),在
按顺时针方向旋转(如图2),在![]() 从
从![]() 到
到![]() 的变化过程中,点
的变化过程中,点![]() 相应移动的路径长共为 .(结果保留根号)
相应移动的路径长共为 .(结果保留根号)
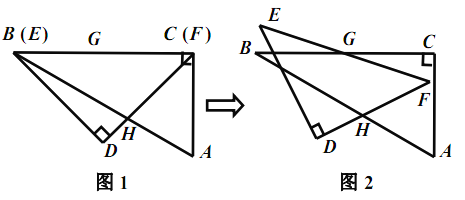
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com