
【题目】根据下面给出的数轴,解答下面的问题:
(1)请你根据图中A、B两点的位置,分别写出它们所表示的有理数A:_____B:_____.
(2)观察数轴,与点A的距离为4的点表示的数是:_____.
(3)若将数轴折叠,使得A点与﹣2表示的点重合,则B点与数_____表示的点重合.
![]()
科目:初中数学 来源: 题型:
【题目】李明同时掷甲、乙两枚质地均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).记甲立方体朝上一面上的数字为x、乙立方体朝上一面朝上的数字为y,这样就确定点P的一个坐标( ![]() ,
, ![]() ),那么点P落在双曲线
),那么点P落在双曲线 ![]() 上的概率为( )
上的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个扇形满足弧长的比等于它们半径的比,则称这两个扇形相似。如图,如果扇形AOB与扇形 ![]() 是相似扇形,且半径
是相似扇形,且半径 ![]() (
( ![]() 为不等于0的常数)。那么下面四个结论:①∠AOB=∠
为不等于0的常数)。那么下面四个结论:①∠AOB=∠ ![]() ;②△AOB∽△
;②△AOB∽△ ![]() ;③
;③ ![]() ;④扇形AOB与扇形
;④扇形AOB与扇形 ![]() 的面积之比为
的面积之比为 ![]() 。成立的个数为:( )
。成立的个数为:( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次点A向左移动3个单位长度到达点A1,第2次从点A1向右移动6个单位长度到达点A2,第3次从点A2向左移动9个单位长度到达点A3,…,按照这种移动规律进行下去,第n次移动到达点An,如果点An与原点的距离不小于50,那么n的最小值是_____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场国庆节搞促销活动,购物不超过200元不给优惠,超过200(不含200元)元而不足500元,所有商品按购物价优惠10%,超过500元的,其中500元按9折优惠,超过的部分按8折优惠,A,B两个商品价格分别为180元,550元。
(1) 某人第一次购买一件A商品,第二次购买一件B商品,实际共付款多少元?
(2) 若此人一次购物购买A,B商品各一件,则实际付款多少钱?
(3) 国庆期间,某人在该商场两次购物分别付款180元和550元,如果他合起来一次性购买同样的商品,还可节约多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、M两点,若点M的坐标是(-4,-2),则点N的坐标为( )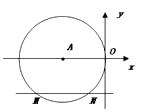
A.(-1,-2)
B.(1,2)
C.(-1.5,-2)
D.(1.5,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好治理西太湖水质,保护环境,市治污公司决定购买10台污水处理设备,现有A、B两种型号的设备,其中每台的价格,月处理污水量如下表:

经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买4台B型设备少4万元.
(1)求a、b的值;
(2)经预算:市治污公司购买污水处理设备的资金不超过47万元,你认为该公司有哪几种购买方案;
(3)在(2)问的条件下,若该月要求处理西太湖的污水量不低于1860吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图17,在△ABC中,D是BC边上的一点,E是AD的中点,过A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:BD=CD.
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
(3)当△ABC满足什么条件时,四边形AFBD为正方形?(写出条件即可,不要求证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学在平时的练习中,遇到下面一道题目:
如图,∠AOC=90°,OE 平分∠BOC,OD平分∠AOB.
①若∠BOC=60°,求∠DOE 度数;
②若∠BOC=α(0<α<90°),其他条件不变,求∠DOE 的度数.
(1)下面是某同学对①问的部分解答过程,请你补充完整.
∵OE 平分∠BOC,∠BOC=60°
∴∠BOE= . (角平分线的定义)
∵∠AOC=90°,∠BOC=60°
∴ ,
∵OD 平分∠AOB,
∴ ,(角平分线的定义)
∴∠DOE= .
(注:符号∵表示因为,用符号∴表示所以).
(2)仿照①的解答过程,完成第②小题.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com