
【题目】如图1,在平面直角坐标系中,O为坐标原点,抛物线y=a(x﹣h)2﹣4(a>0)与x轴分别交于原点O、A两点,点A在x轴的正半轴上,顶点为D,直线y= ![]() x交抛物线于B点,过B作BE∥x轴交抛物线另一点E,交对称轴于F.
x交抛物线于B点,过B作BE∥x轴交抛物线另一点E,交对称轴于F.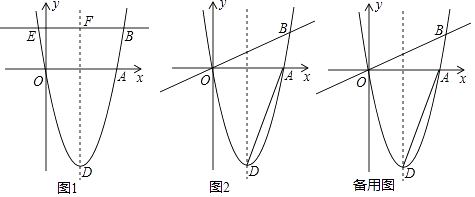
(1)当DF=4a时,求BE的长.
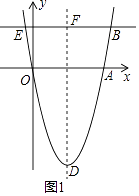
(2)如图2,连AD,连接AD绕点A旋转交直线OB于点G,点D的对应点为G,当OG=2时,求a的值;
(3)在(2)的条件下,当0<a<1时,以OB为直径作圆交x轴下方抛物线于点P,求点P坐标.
【答案】
(1)解:如图1中,
由题意D(h,﹣4),
∵DF=4a,
∴点F坐标(h,4a﹣4),
当y=4a﹣4时,4a﹣4=a(x﹣h)2﹣4,
解得x=h±2,
∴B(2+h,4a﹣4),E(h﹣2,4a﹣4),
∴BE=(2+h)﹣(h﹣2)=4.
(2)解:如图2中,由题意OG=2,可得G(﹣ ![]() ,﹣1)或G′(
,﹣1)或G′( ![]() ,1).
,1).
当AD=AG,A(2h,0),D(h,﹣4),
∴(2h+ ![]() )2+1=h2+16,
)2+1=h2+16,
∴h= ![]() 或﹣2
或﹣2 ![]() (舍弃),
(舍弃),
∴A( ![]() ,0),代入y=a(x﹣h)2﹣4,解得a=3,
,0),代入y=a(x﹣h)2﹣4,解得a=3,
当AD=AG′时,(2h﹣ ![]() )2+1=h2+16,
)2+1=h2+16,
解得h=2 ![]() 或﹣
或﹣ ![]() (舍弃),
(舍弃),
∴A(4 ![]() ,0),代入y=a(x﹣h)2﹣4,解得a=
,0),代入y=a(x﹣h)2﹣4,解得a= ![]() ,
,
综上所述,A的值为3或 ![]() .
.
(3)解:由题意抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x,
x,
由 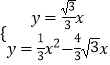 ,解得
,解得 ![]() ,或
,或 ![]() ,
,
∴B(5 ![]() ,5),
,5),
∴OB=10,
∴线段OB的中点O′( ![]() ,
, ![]() )
)
设P(m, ![]() m2﹣
m2﹣ ![]() m),
m),
由题意PO′=5,
∴(m﹣ ![]() )2+(
)2+( ![]() m2﹣
m2﹣ ![]() m﹣
m﹣ ![]() )2=52,
)2=52,
∴m2﹣5 ![]() m+
m+ ![]() +(
+( ![]() m2﹣
m2﹣ ![]() m)2﹣5(
m)2﹣5( ![]() m2﹣
m2﹣ ![]() m)+
m)+ ![]() =25,
=25,
∴m2﹣5 ![]() m+(
m+( ![]() m2﹣
m2﹣ ![]() m)(
m)( ![]() m2﹣
m2﹣ ![]() m﹣5)=0,
m﹣5)=0,
∴m2﹣5 ![]() m+
m+ ![]() m(m﹣4
m(m﹣4 ![]() )(m﹣5
)(m﹣5 ![]() )(m+
)(m+ ![]() )=0
)=0
∴ ![]() m(m﹣5
m(m﹣5 ![]() )(m2﹣3
)(m2﹣3 ![]() m﹣3)=0
m﹣3)=0
∴m=0或5 ![]() 或
或 ![]() 或
或 ![]() ,
,
∵点P在x轴下方,
∴P( ![]() ,
, ![]() ).
).
【解析】(1)由顶点式求出D(h,-4),再表示出B纵坐标,y=4a﹣4代入解析式,求出B、E两点的横坐标,求出其差,就是BE;(2)AD绕点A旋转交直线OB于点G,位置有两个,分类讨论,利用两点间距离公式列出方程,求出a值;(3)求出OB的中点,就是圆心,利用“圆上任意点到圆心距离等于半径”及两点间距离公式,列出方程,求出P的横坐标m.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将三角形ABC向左平移至点B与原点重合,得三角形A′OC′.
(1)直接写出三角形ABC的三个顶点的坐标A B C ;
(2)画出三角形A′OC′;
(3)求三角形ABC的面积;
(4)直接与出A′C′与y轴交点的坐标 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市少年宫准备组织市区部分学校的中小学生到本市A,B,C,D,E五个旅游景区“一日游”,每名学生只能在五个景区中任选一个,为估算到各景区“一日游”的学生人数,少年宫随机抽取这些学校的部分学生,进行了“五个景区你最想去那里”的问卷调查,并把统计结果绘制成如图所示的统计图.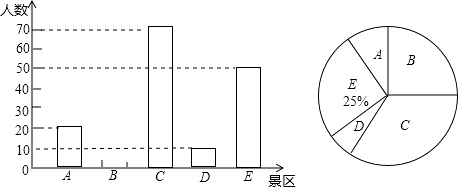
(1)求参加问卷调查的学生数,并将条形统计图补充完整;
(2)若参加“一日游”的学生为1000人,请估计到C景区“一日游”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 75 | 80 | 90 |
面试 | 93 | 70 | 68 |
根据录用程序,学校组织200名学生采用投票推荐的方式,对三人进行民主测评,三人得票率(没有弃权,每位同学只能推荐1人)如扇形统计图所示,每得一票记1分.
(1)扇形统计图中![]() = , 分别计算三人民主评议的得分;
= , 分别计算三人民主评议的得分;
(2)根据实际需要,学校将笔试、面试、民主评议三项得分按4:3:3的比例确定个人成绩,得分最高者将被选中,通过计算说明三人中谁被选中?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,老师给出了如下问题:如图,∠AOB=80°,OC平分∠AOB,若∠BOD=20°.
(1)请你补全图形,并求∠COD的度数;
(2)若∠BOD=![]() 其他条件不变,请直接写出∠COD的度数.
其他条件不变,请直接写出∠COD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,教师出示某区篮球赛积分表如下:

(1)从表中可以看出,负一场积多少分,胜一场积多少分;
(2)请你帮忙算出二队胜了多少场?
(3)在这次比赛中,一个队胜场总积分能不能等于它的负场总积分?
(4)在计算五队、六队胜出场次的时候,老师还没等同学们计算出来就立刻说出了答案,老师解释说:“我是通过找到积分与胜场之间的数量关系求出来的”,请你说出其中的奥秘.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两地相距4km,上午8:00时,亮亮从A地步行到B地,8:20时芳芳从B地出发骑自行车到A地,亮亮和芳芳两人离A地的距离S(km)与亮亮所用时间t(min)之间的函数关系如图所示,芳芳到达A地时间为( )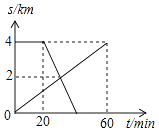
A.8:30
B.8:35
C.8:40
D.8:45
查看答案和解析>>
科目:初中数学 来源: 题型:
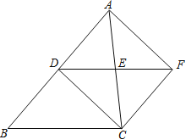
【题目】如图,在△ABC中,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得到△CFE.
(1)求证:四边形ADCF是平行四边形.
(2)当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“父母恩深重,恩怜无歇时”,每年5月的第二个星期日即为母亲节,节日前夕巴蜀中学学生会计划采购一批鲜花礼盒赠送给妈妈们.
(1)经过和花店卖家议价,可在原标价的基础上打八折购进,若在花店购买80个礼盒最多花费7680元,请求出每个礼盒在花店的最高标价;(用不等式解答)
(2)后来学生会了解到通过“大众点评”或“美团”同城配送会在(1)中花店最高售价的基础上降价25%,学生会计划在这两个网站上分别购买相同数量的礼盒,但实际购买过程中,“大众点评”网上的购买价格比原有价格上涨 ![]() m%,购买数量和原计划一样:“美团”网上的购买价格比原有价格下降了
m%,购买数量和原计划一样:“美团”网上的购买价格比原有价格下降了 ![]() m元,购买数量在原计划基础上增加15m%,最终,在两个网站的实际消费总额比原计划的预算总额增加了
m元,购买数量在原计划基础上增加15m%,最终,在两个网站的实际消费总额比原计划的预算总额增加了 ![]() m%,求出m的值.
m%,求出m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com