
 如图,边长为2的等边△ABC和边长为1的等边△A′B′C′,它们的边B′C′,BC位于同一条直线l上,开始时,点C′与B重合,△ABC固定不动,然后把△A′B′C′自左向右沿直线l平移,移出△ABC外(点B′与C重合)停止,设△A′B′C′平移的距离为x,两个三角形重合部分的面积为y,则y关于x的函数图象是( )
如图,边长为2的等边△ABC和边长为1的等边△A′B′C′,它们的边B′C′,BC位于同一条直线l上,开始时,点C′与B重合,△ABC固定不动,然后把△A′B′C′自左向右沿直线l平移,移出△ABC外(点B′与C重合)停止,设△A′B′C′平移的距离为x,两个三角形重合部分的面积为y,则y关于x的函数图象是( )| A. |  | B. |  | C. |  | D. |  |
分析 分为0<x≤1、1<x≤2、2<x≤3三种情况画出图形,然后依据等边三角形的性质和三角形的面积公式可求得y与x的函数关系式,于是可求得问题的答案.
解答 解:如图1所示:当0<x≤1时,过点D作DE⊥BC′.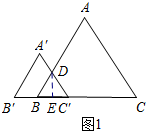
∵△ABC和△A′B′C′均为等边三角形,
∴△DBC′为等边三角形.
∴DE=$\frac{\sqrt{3}}{2}$BC′=$\frac{\sqrt{3}}{2}$x.
∴y=$\frac{1}{2}$BC′•DE=$\frac{\sqrt{3}}{4}$x2.
当x=1时,y=$\frac{\sqrt{3}}{4}$,且抛物线的开口向上.
如图2所示:1<x≤2时,过点A′作A′E⊥B′C′,垂足为E.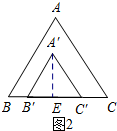
∵y=$\frac{1}{2}$B′C′•A′E=$\frac{1}{2}$×1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$.
∴函数图象是一条平行与x轴的线段.
如图3所示:2<x≤3时,过点D作DE⊥B′C,垂足为E.
y=$\frac{1}{2}$B′C•DE=$\frac{\sqrt{3}}{4}$(x-3)2,函数图象为抛物线的一部分,且抛物线开口向上.
故选:B.
点评 本题主要考查的是动点问题的函数图象,求得函数的解析式是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com