
【题目】我们规定:三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差.如图1,在△ABC中,AO是BC边上的中线,AB与AC的“极化值”就等于AO2﹣BO2的值,可记为AB△AC=AO2﹣BO2 .
(1)在图1中,若∠BAC=90°,AB=8,AC=6,AO是BC边上的中线,则AB△AC= , OC△OA=;
(2)如图2,在△ABC中,AB=AC=4,∠BAC=120°,求AB△AC、BA△BC的值;
(3)如图3,在△ABC中,AB=AC,AO是BC边上的中线,点N在AO上,且ON= ![]() AO.已知AB△AC=14,BN△BA=10,求△ABC的面积.
AO.已知AB△AC=14,BN△BA=10,求△ABC的面积.
【答案】
(1)0;7
(2)
解:①如图2,取BC的中点O,连接AO,
∵AB=AC,
∴AO⊥BC,
在△ABC中,AB=AC,∠BAC=120°,
∴∠ABC=30°,
在Rt△AOB中,AB=4,∠ABC=30°,
∴AO=2,OB=2 ![]() ,
,
∴AB△AC=AO2﹣BO2=4﹣12=﹣8,
②取AC的中点D,连接BD,
∴AD=CD= ![]() AC=2,
AC=2,
过点B作BE⊥AC交CA的延长线于E,
在Rt△ABE中,∠BAE=180°﹣∠BAC=60°,
∴∠ABE=30°,
∵AB=4,
∴AE=2,BE=2 ![]() ,
,
∴DE=AD+AE=4,
在Rt△BED中,根据勾股定理得,BD= ![]() =
= ![]() =2
=2 ![]() ,
,
∴BA△BC=BD2﹣CD2=24;
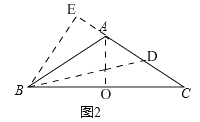
(3)
解:如图3,
设ON=x,OB=OC=y,
∴BC=2y,OA=3x,
∵AB△AC=14,
∴OA2﹣OB2=14,
∴9x2﹣y2=14①,
取AN的中点D,连接BD,

∴AD=DB= ![]() AN=
AN= ![]() ×
× ![]() OA=ON=x,
OA=ON=x,
∴OD=ON+DN=2x,
在Rt△BOD中,BD2=OB2+OD2=y2+4x2,
∵BN△BA=10,
∴BD2﹣DN2=10,
∴y2+4x2﹣x2=10,
∴3x2+y2=10②
联立①②得, ![]() 或
或 ![]() (舍),
(舍),
∴BC=4,OA=3 ![]() ,
,
∴S△ABC= ![]() BC×AO=6
BC×AO=6 ![]() .
.
【解析】解:①∵∠BAC=90°,AB=8,AC=6,
∴BC=10,
∵点O是BC的中点,
∴OA=OB=OC= ![]() BC=5,
BC=5,
∴AB△AC=AO2﹣BO2=25﹣25=0,②如图1,
取AC的中点D,连接OD,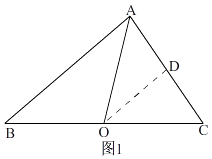
∴CD= ![]() AC=3,
AC=3,
∵OA=OC=5,
∴OD⊥AC,
在Rt△COD中,OD= ![]() =4,
=4,
∴OC△OA=OD2﹣CD2=16﹣9=7,
故答案为0,7;
(1)①先根据勾股定理求出BC=10,再利用直角三角形的性质得出OA=OB=OC=5,最后利用新定义即可得出结论;②再用等腰三角形的性质求出CD=3,再利用勾股定理求出OD,最后用新定义即可得出结论;(2)①先利用含30°的直角三角形的性质求出AO=2,OB=2 ![]() ,再用新定义即可得出结论;②先构造直角三角形求出BE,AE,再用勾股定理求出BD,最后用新定义即可得出结论;(3)先构造直角三角形,表述出OA,BD2 , 最后用新定义建立方程组求解即可得出结论.
,再用新定义即可得出结论;②先构造直角三角形求出BE,AE,再用勾股定理求出BD,最后用新定义即可得出结论;(3)先构造直角三角形,表述出OA,BD2 , 最后用新定义建立方程组求解即可得出结论.


科目:初中数学 来源: 题型:
【题目】(本小题满分8分)
阅读材料:
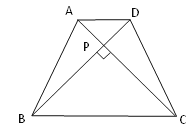
如图,在四边形ABCD中,对角线AC⊥BD,垂足为P.
求证:S四边形ABCD=![]()
证明:AC⊥BD→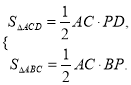
∴S四边形ABCD=S△ACD+S△ACB= ![]()
=![]()
解答问题:
(1)上述证明得到的性质可叙述为_______________________________________.
(2)已知:如图,等腰梯形ABCD中,AD∥BC,对角线AC⊥BD且相交于点P,AD=3cm,BC=7cm,利用上述的性质求梯形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注.某单位计划在室内安装空气净化装置,需购进A、B两种设备.每台B种设备价格比每台A种设备价格多0.7万元,花3万元购买A种设备和花7.2万元购买B种设备的数量相同.
(1)求A种、B种设备每台各多少万元?
(2)根据单位实际情况,需购进A、B两种设备共20台,总费用不高于15万元,求A种设备至少要购买多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
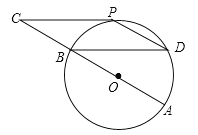
【题目】如图,⊙O的直径AB=12cm,C为AB延长线上一点,CP与⊙O相切于点P,过点B作弦BD∥CP,连接PD.
(1)求证:点P为![]() 的中点;
的中点;
(2)若∠C=∠D,求四边形BCPD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围;
(3)当△ADE是等腰三角形时,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某实验学校准备在“十一”黄金周组织部分教师到陕西安康旅游,现联系了甲、乙两旅行社,两家旅行社报价均为400元/人,同时两旅行社对10人以上的团体推出了优惠举措:甲旅行社对每位游客七五折优惠;乙旅行社是免去一位带队老师的费用,其余的八折优惠①求人数为多少时,两家旅行社的收费相同?②请你通过计算说明:旅游人数在什么范围时选择甲旅行社费用较少?旅游人数在什么范围时选择乙旅行社的费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市双城同创的工作中,某社区计划对1200m2的区域进行绿化,经投标,由甲、乙两个施工队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为300m2区域的绿化时,甲队比乙队少用3天.
(1)甲、乙两施工队每天分别能完成绿化的面积是多少?
(2)设先由甲队施工x天,再由乙队施工y天,刚好完成绿化任务,求y与x的函数关系式.
(3)若甲队每天绿化费用为0.4万元,乙队每天绿化费用为0.15万元,且甲、乙两队施工的总天数不超过14天,则如何安排甲、乙两队施工的天数,使施工费用最少?并求出最少费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com