
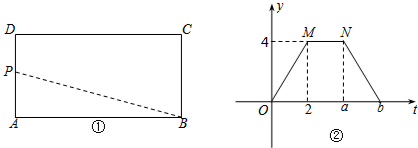
分析 (1)从图②中根据面积和运动时间求出AD,AB,从而得到a,b;
(2)从图②中点N的纵坐标和横坐标分别考虑,结合图①即可;
(3)y是2cm2的话,由于AB=4,只有点P到AB的距离为1,即可.
解答 解:(1)由图②中发现,点P从开始运动到2s时运动到点D,且在AD边上速度为1,
∴BC=AD=2,
∵点P在DC上运动时,面积不变是4,
∴4=$\frac{1}{2}$AB×AD,
∴AB=4,
∵DC上的运动速度为2cm/s,
∴a=2+4÷2=4,
∴b=2+2+2=6,
故答案为4,6;
(2)P运动了4s时到达点C,此时△PAB的面积为4cm2,
(3)由题意AB=DC=4,
∵要y的值为2cm2,即点P到AB的距离为1,
∴必须点P在AD或BC上,且PA=1cm或PB=1cm,
当PA=1cm时,点P的运动时间t=1s,
当PB=1cm时,点P的运动时间为t=6-1=5s,
即当t为1s或5s时,y的值为2cm2.
点评 此题是四边形综合题,主要考查的是动点问题,解本题的关键是从图中找到对应的量,也是解本题的难点.


科目:初中数学 来源: 题型:选择题
| A. | 在装有5个红球的袋中摸出1个球,是红球 | |
| B. | 小麦的亩产量一定为1500千克 | |
| C. | 打开电视机,正在转播足球比赛 | |
| D. | 农历十五的晚上一定能看到圆月 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-x-y)(x+y) | B. | (2x-y)(y-2x) | C. | (1-$\frac{1}{2}$x)(-1-$\frac{1}{2}$x) | D. | (3x+y)(x-3y) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
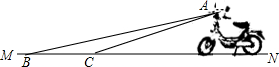 齐河路路通电动车厂新开发的一种电动车如图,它的大灯A射出的光线AB,AC 与地面MN 所夹的锐角分别为8°和10°,大灯A与地面的距离为1m则该车大灯照亮地面的宽度BC是1.4m.(不考虑其它因素)
齐河路路通电动车厂新开发的一种电动车如图,它的大灯A射出的光线AB,AC 与地面MN 所夹的锐角分别为8°和10°,大灯A与地面的距离为1m则该车大灯照亮地面的宽度BC是1.4m.(不考虑其它因素)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
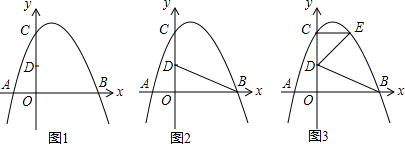
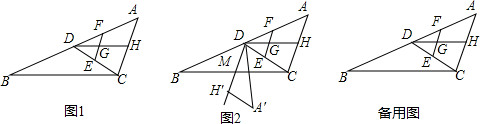 如图1,在△ABC中,CD为AB边上的中线,点E、F分别在线段CD、AD上,且$\frac{DF}{DB}=\frac{DE}{DC}$.点G是EF的中点,射线DG交AC于点H.
如图1,在△ABC中,CD为AB边上的中线,点E、F分别在线段CD、AD上,且$\frac{DF}{DB}=\frac{DE}{DC}$.点G是EF的中点,射线DG交AC于点H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com