
分析 由方程有两个相等的实数根,可得出△=0且二次项系数≠0,解方程和不等式即可得出k值,将其代入原方程中,解方程即可得出结论.
解答 解:∵关于x的方程(k-1)x2-(k-1)x+$\frac{1}{4}$=0有两个相等的实数根,
∴$\left\{\begin{array}{l}{△=0}\\{k-1≠0}\end{array}\right.$,即$\left\{\begin{array}{l}{[-(k-1)]^{2}-4(k-1)×\frac{1}{4}=0}\\{k-1≠0}\end{array}\right.$,
解得:k=2.
当k=2时,原方程为x2-x+$\frac{1}{4}$=$(x-\frac{1}{2})^{2}$=0,
解得:x1=x2=$\frac{1}{2}$.
点评 本题考查了根的判别式,解题的关键是由方程由两个相等的实数根得出关于k的一元二次方程即一元一次不等式.本题属于基础题,难度不大,解决该题型题目时,根据根的个数结合根的判别式,得出不等式(方程或方程组)是关键.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:填空题
 如图,在直升机的镜头下,观测A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是200($\sqrt{3}$+1)米.
如图,在直升机的镜头下,观测A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是200($\sqrt{3}$+1)米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分.某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知A,B两组户数频数直方图的高度比为1:5.
在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分.某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知A,B两组户数频数直方图的高度比为1:5.| 组别 | 消费额(元) |
| A | 10≤x<100 |
| B | 100≤x<200 |
| C | 20≤x<300 |
| D | 300≤x<400 |
| E | x≥400 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
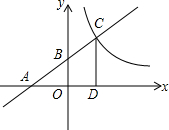 已知函数y1=$\frac{2}{3}$x+2的图象分别与坐标轴相交于A,B两点(如图所示),与反比例函数y2=$\frac{k}{x}$(x>0)的图象相交于C点.
已知函数y1=$\frac{2}{3}$x+2的图象分别与坐标轴相交于A,B两点(如图所示),与反比例函数y2=$\frac{k}{x}$(x>0)的图象相交于C点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
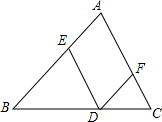 已知D为△ABC边BC上的一个动点(不与B,C重合),过D作DE∥AC交AB于点E,作DF∥AB交AC于点F.
已知D为△ABC边BC上的一个动点(不与B,C重合),过D作DE∥AC交AB于点E,作DF∥AB交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com