
分析 根据平均每天销售量=90-超过50元的价格×3,则该批发商平均每天的销售利润w(元)=每箱的销售利润×每天的销售量,再根据题中所给的自变量的取值得到二次的最值问题即可.
解答 解:由题意得:90-3(x-50)
∴y=(x-40)(-3x+240)
=-3x2+360x-9600,
∵a<0
∴抛物线开口向下.
当x=-$\frac{b}{2a}$=60时,y有最大值.
又∵x<60,y随x的增大而增大.
∴当x=55元时,y的最大值为1125元.
∴当每箱苹果的销售价为55元时,可以获得1125元的最大利润.
点评 此题考查了二次函数的性质在实际生活中的应用.最大销售利润的问题常用函数的增减性来解答,要注意应该在自变量的取值范围内求最大值(或最小值),也就是说二次函数的最值不一定在x=-$\frac{b}{2a}$时取得.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∠A=∠D | B. | ∠C=∠F | C. | ∠B=∠E | D. | ∠C=∠D |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
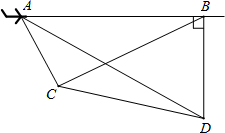 如图,一架飞机以200米/秒的速度由A向B沿水平直线方向飞行,在航线AB的下方有两个山头C、D,飞机在A处时,测得山头C、D在飞机的前方,俯角分别为60°和30°.飞机飞行1分钟后到B处时,往后测得山头C的俯角为30°,而山头D恰好在飞机的正下方.求山头C、D之间的距离.
如图,一架飞机以200米/秒的速度由A向B沿水平直线方向飞行,在航线AB的下方有两个山头C、D,飞机在A处时,测得山头C、D在飞机的前方,俯角分别为60°和30°.飞机飞行1分钟后到B处时,往后测得山头C的俯角为30°,而山头D恰好在飞机的正下方.求山头C、D之间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 先向左平移2个单位,再向上平移4个单位 | |
| B. | 先向左平移2个单位,再向下平移4个单位 | |
| C. | 先向右平移2个单位,再向下平移4个单位 | |
| D. | 先向右平移2个单位,再向上平移4个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com