
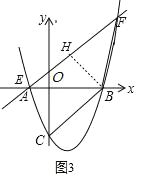
【题目】如图,已知:抛物线y=a(x+1)(x﹣3)与x轴相交于A、B两点,与y轴的交于点C(0,﹣3).
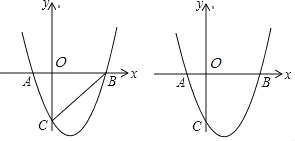
(1)求抛物线的解析式的一般式.
(2)若抛物线上有一点P,满足∠ACO=∠PCB,求P点坐标.
(3)直线l:y=kx﹣k+2与抛物线交于E、F两点,当点B到直线l的距离最大时,求△BEF的面积.
【答案】(1)y=x2﹣2x﹣3;(2)(4,5)或(![]() );(3)10
);(3)10
【解析】
(1)把C点坐标代入y=a(x+1)(x-3)中求出a的值即可得到抛物线解析式;
(2)分两种情况,当点P在直线BC的下方时,过点B作BE⊥BC交CP的延长线于点E,过点E作EM⊥x轴于点M,由直角三角形的性质可求得ME,BM长,求出点E的坐标,可求出直线CE的解析式,联立直线和抛物线方程可求出点P的坐标;当点P在直线BC的上方时,过点B作BF⊥BC交CP于点F,同理求出点F的坐标和直线CF的解析式,联立直线和抛物线方程可求得点P的坐标;
(3)求出直线y=kx-k+2恒过定点H(1,2),连结BH,当BH⊥直线l时,点B到直线l的距离最大时,求出此时k的值,可求出点E,F的坐标,则△BEF的面积可求出.
解:(1)把C(0,﹣3)代入y=a(x+1)(x﹣3),
得﹣3a=﹣3,解得a=1,
所以抛物线解析式为y=(x+1)(x﹣3),即y=x2﹣2x﹣3;
(2)当点P在直线BC的下方时,如图1,过点B作BE⊥BC交CP的延长线于点E,过点E作EM⊥x轴于点M,
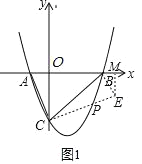
∵y=(x+1)(x﹣3),
∴y=0时,x=﹣1或x=3,
∴A(﹣1,0),B(3,0),
∴![]() ,
,
∵OB=OC=3,
∴∠ABC=45°,![]() ,
,
∵∠ACO=∠PCB,
∴![]() ,
,
∴![]() ,
,
∵∠CBE=90°,
∴∠MBE=45°,
∴BM=ME=1,
∴E(4,﹣1),
设直线CE的解析式为y=kx+b,
∴![]() ,
,
解得: ,
,
∴直线CE的解析式为![]() ,
,
∴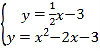 ,
,
解得![]() ,
,![]() ,
,
把![]() 代入
代入![]() 得
得![]() ,
,
∴![]() ,
,
当点P在直线BC的上方时,过点B作BF⊥BC交CP于点F,如图2,

同理求出![]() ,FN=BN=1,
,FN=BN=1,
∴F(2,1),
求出直线CF的解析式为y=2x﹣3,
∴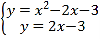 ,
,
解得:x1=0,x2=4,
∴P(4,5).
综合以上可得点P的坐标为(4,5)或(![]() );
);
(3)∵直线l:y=kx﹣k+2,
∴y﹣2=k(x﹣1),
∴x﹣1=0,y﹣2=0,
∴直线y=kx﹣k+2恒过定点H(1,2),如图3,连结BH,当BH⊥直线l时,点B到直线l的距离最大时,
求出直线BH的解析式为y=﹣x+3,
∴k=1,
∴直线l的解析式为y=x+1,
∴![]() ,
,
解得: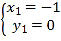 ,
,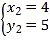 ,
,
∴E(﹣1,0),F(4,5),
∴![]() .
.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
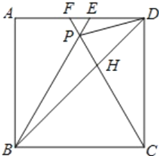
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论,其中正确结论的个数是( )
①△BDE∽△DPE;②![]() ;③
;③![]() ;④tan∠DBE=
;④tan∠DBE=![]() .
.
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,对角线AC与BD相交于点O,再添加一个条件,仍不能判定四边形ABCD是矩形的是 ( )
A.AB=ADB.OA=OBC.AC=BDD.DC⊥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() ,点
,点![]() ,与y轴交于点C,且过点
,与y轴交于点C,且过点![]() .点P、Q是抛物线
.点P、Q是抛物线![]() 上的动点.
上的动点.
(1)求抛物线的解析式;
(2)当点P在直线OD下方时,求![]() 面积的最大值.
面积的最大值.
(3)直线OQ与线段BC相交于点E,当![]() 与
与![]() 相似时,求点Q的坐标.
相似时,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里有1个红球,1个黄球和n个白球,它们除颜色外其余都相同.
(1)从这个袋子里摸出一个球,记录其颜色,然后放回,摇均匀后,重复该实验,经过大量实验后,发现摸到白球的频率稳定于0.5左右,求n的值;
(2)在(1)的条件下,先从这个袋中摸出一个球,记录其颜色,放回,摇均匀后,再从袋中摸出一个球,记录其颜色.请用画树状图或者列表的方法,求出先后两次摸出不同颜色的两个球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
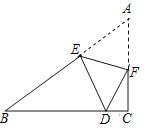
【题目】如图在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点E、F分别在边AB、AC上,将△AEF沿直线EF折叠,使点A的对应点D恰好落在边BC上.若△BDE是直角三角形,则CF的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=ax2+bx+c(a≠0)的部分图象如图所示:
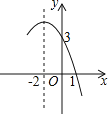
①当y<0时,x的取值范围是______;
②方程ax2+bx+c=3的解是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长,中华汉字,寓意深广.为传承中华优秀传统文化,某中学德育处组织了一次全校2000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,学校德育处随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
成绩x(分)分数段 | 频数(人) | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | 0.2 |
80≤x<90 | m | 0.35 |
90≤x<100 | 50 | n |
频数分布直方图

根据所给的信息,回答下列问题:
(1)m=________;n=________;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在________分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的2000名学生中成绩是“优”等的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
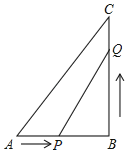
【题目】如图,在Rt△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向终点B以1cm/s的速度移动,点Q从点B开始沿BC边向终点C以2cm/s的速度移动,当其中一点到达终点时,另一点随之停止.点P,Q分别从点A,B同时出发.
(1)求出发多少秒时PQ的长度等于5cm;
(2)出发 秒时,△BPQ中有一个角与∠A相等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com