
分析 (1)由根的判别式可知b2-4ac=m2,结合2次方的非负性即可证出结论;
(2)由根与系数的关系可得出x1+x2=-$\frac{b}{a}$=8,套入数据即可得出关于m的一元一次方程,解方程即可得出结论.
解答 (1)证明:△=b2-4ac=(m-1)2-4×$\frac{1}{4}$(-2m+1)=m2-2m+1+2m-1=m2.
∵m≠0,
∴m2>0,
∴当m≠0时,原方程总有两个不相等的实数根.
(2)解:由已知得:x1+x2=-$\frac{b}{a}$=-4(m-1)=8,
即m+1=0,解得:m=-1.
答:若原方程的两根之和为8,则m的值为-1.
点评 本题考查了根与系数的关系、根的判别式以及解一元一次方程,解题的关键是:(1)找出b2-4ac=m2;(2)得处关于m的一元一次方程.本题属于基础题,难度不大,解决该题型题目时,根据根与系数的关系找出两根之和与两根之积是关键.


科目:初中数学 来源: 题型:解答题
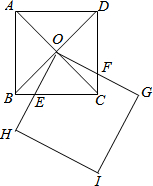 在边长为2的正方形ABCD中,对角线AC与BD相交于点O,另一个正方形OHIG绕点O旋转(如图),设OH与边BC交于点E(与点B、C不重合),OG与边CD交于点F.
在边长为2的正方形ABCD中,对角线AC与BD相交于点O,另一个正方形OHIG绕点O旋转(如图),设OH与边BC交于点E(与点B、C不重合),OG与边CD交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
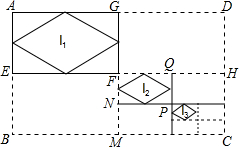 如图,在矩形ABCD中,AD=a,AB=b,连接其对边中点,得到四个矩形,顺次连接矩形AEFG各边中点,得到菱形I1;连接矩形FMCH对边中点,又得到四个矩形,顺次连接矩形FNPQ各边中点,得到菱形I2;…如此操作下去,得到菱形I2016,则I2016的面积是($\frac{1}{2}$)4033ab.
如图,在矩形ABCD中,AD=a,AB=b,连接其对边中点,得到四个矩形,顺次连接矩形AEFG各边中点,得到菱形I1;连接矩形FMCH对边中点,又得到四个矩形,顺次连接矩形FNPQ各边中点,得到菱形I2;…如此操作下去,得到菱形I2016,则I2016的面积是($\frac{1}{2}$)4033ab.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
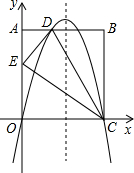 如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.
如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com