
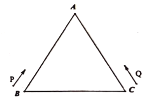
【题目】如图,等边三角形![]() 的周长为
的周长为![]() ,
,![]() ,
,![]() 两点分别从
两点分别从![]() ,
,![]() 两点同时出发,点
两点同时出发,点![]() 以
以![]() 的速度按顺时针方向在三角形的边上运动,点
的速度按顺时针方向在三角形的边上运动,点![]() 以
以![]() 的速度按逆时针方向在三角形的边上运动.设
的速度按逆时针方向在三角形的边上运动.设![]() ,
,![]() 两点第一次在三角形
两点第一次在三角形![]() 的顶点处相遇的时间为
的顶点处相遇的时间为![]() ,第二次在三角形
,第二次在三角形![]() 顶点处相遇的时间为
顶点处相遇的时间为![]() ,则
,则![]() _______.
_______.
科目:初中数学 来源: 题型:
【题目】为提高学生的爱国意识,陶冶爱国情操,某中学举行了以“厉害了,我的国”为主题的书法绘画大赛,该校九年级共有三个班都参加了这次活动,三个班根据初赛成绩分别选出了10名同学参加决赛,这些选手的决赛成绩(满分100分)如下表所示:
收集数据:

数据
(1)请填写下表:
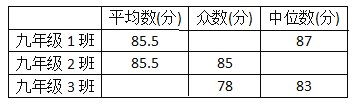
得出结论:
(2)如果在每个班级参加决赛的选手中分别选出3人参加总决赛,你认为哪个班级的实力更强一些?请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学社团活动中,指导老师给同学们提出了以下问题:
问题:有67张卡片叠在一起,按从上而下的顺序先把第一张拿走,把第二张放到底层,然后把第三张拿走,再把第四张放到底层,如此进行下去,直至只剩最后一张卡片.问仅剩的这张卡片是原来的第几张卡片?
由于卡片数量较多,指导老师建议同学们先对较少的张数进行尝试,以便熟悉游戏规则并发现一些规律!
(1)请你试着在草稿纸上进行试验,将试验结果填写在下表中:
试验的卡片数量 (张) | 2 | 4 | 8 | 9 | 10 | 11 |
剩下最后一张卡片是 原来卡片的第几张 |
(2)根据试验结果的规律,回答最初的67张卡片情形,请你给出答案并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租车司机从公司出发,在东西方向的人民路上连续接送![]() 批客人,行驶路程记录如下(规定向东为正,向西为负,单位:
批客人,行驶路程记录如下(规定向东为正,向西为负,单位:![]() ):
):
第 | 第 | 第 | 第 | 第 |
|
|
|
|
|
(1)接送完第![]() 批客人后,该驾驶员在公司什么方向,距离公司多少千米?
批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)若该出租车每千米耗油![]() 升,那么在这过程中共耗油多少升?
升,那么在这过程中共耗油多少升?
(3)若该出租车的计价标准为:行驶路程不超过![]() 收费
收费![]() 元,超过
元,超过![]() 的部分按每千米
的部分按每千米![]() 元收费,在这过程中该驾驶员共收到车费多少元?
元收费,在这过程中该驾驶员共收到车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】幻方的历史很悠久,传说中最早出现在夏禹时代的“洛书”,用今天的数学符号翻译出来,就是一个三阶幻方,即将若干个数组成一个正方形数阵,任意一行、一列及对角线上的数字之和都相等.观察下图:

(1)若图1为“和![]() 幻方”,则
幻方”,则![]() ,
,![]() ,
,![]() ;
;

(2)若图2为“和![]() 幻方”,请通过观察上图的 三个幻方,试着用含
幻方”,请通过观察上图的 三个幻方,试着用含![]() 、
、![]() 的代数式表示
的代数式表示![]() ,并说明理由.
,并说明理由.

(3)若图3为“和![]() 幻方”,且
幻方”,且![]() 为整数,试求出所有满足条件的整数
为整数,试求出所有满足条件的整数![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 的顶点
的顶点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 轴的正半抽上,点
轴的正半抽上,点![]() 是
是![]() 上的一点,
上的一点,![]() ,点
,点![]() 的坐标为
的坐标为![]() .动点
.动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿线段
个单位长度的速度沿线段![]() 向点
向点![]() 运动,过点
运动,过点![]() 作
作![]() 的垂线
的垂线![]() 交线段
交线段![]() 于点
于点![]() ,以线段
,以线段![]() 为斜边向右作等腰直角
为斜边向右作等腰直角![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒(
秒(![]() ).
).
(1) 点F的坐标为( , )点![]() 的坐标为( , )(用含
的坐标为( , )(用含![]() 的代数式表示),
的代数式表示),
(2)连接![]() 、
、![]() ,当
,当![]() 为何值时,以
为何值时,以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?
相似?
(3)设点![]() 从点
从点![]() 出发时,点
出发时,点![]() 、
、![]() 、
、![]() 都与点
都与点![]() 重合,点
重合,点![]() 在运动过程中,当
在运动过程中,当![]() 的面积为
的面积为![]() 时,求点
时,求点![]() 运动的时间
运动的时间![]() 的值﹒
的值﹒
查看答案和解析>>
科目:初中数学 来源: 题型:
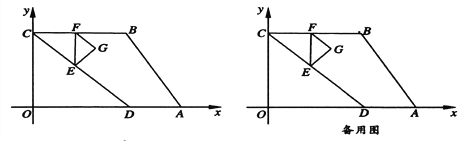
【题目】如图1,在平面直角坐标系中,抛物线过原点O,点A(10,0)和点B(2,2),在线段OA上,点P从点O向点A运动,同时点Q从点A向点O运动,运动过程中保持AQ=2OP,当P、Q重合时同时停止运动,过点Q作x轴的垂线,交直线AB于点M,延长QM到点D,使MD=MQ,以QD为对角线作正方形QCDE(正方形QCDE随点Q运动).
(1)求这条抛物线的函数表达式;
(2)设正方形QCDE的面积为S,P点坐标(m,0)求S与m之间的函数关系式;
(3)过点P作x轴的垂线,交抛物线于点N,延长PN到点G,使NG=PN,以PG为对角线作正方形PFGH(正方形PFGH随点P运动),当点P运动到点(2,0)时,如图2,正方形PFGH的边GF和正方形QCDE的边EQ落在同一条直线上.
①则此时两个正方形中在直线AB下方的阴影部分面积的和是多少?
②若点P继续向点A运动,还存在两个正方形分别有边落在同一条直线上的情况,请直接写出每种情况下点P的坐标,不必说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com