
【题目】填空:如图,已知DG⊥BC,BC⊥AC,EF⊥AB,∠1=∠2,试判断CD与AB的位置关系:

解:CD⊥AB
∵DG⊥BC,BC⊥AC(已知)
∴∠DGB=∠_____=90°(垂直定义)
∴DG∥AC,(____________________)
∴∠2=∠_________.(两直线平行,内错角相等)
∵∠1=∠2(已知)
∴∠1=∠________(等量代换)
∴EF∥______(同位角相等,两直线平行)
∴∠AEF=∠ADC,(________________)
∵EF⊥AB,
∴∠AEF=90°
∴∠ADC=90°
即:CD⊥AB.
【答案】∠ACB;同位角相等,两直线平行;∠ACD;∠ACD;CD;两直线平行,同位角相等.
【解析】
根据垂直于同一直线的两条直线平行,证出DG∥AC,再根据DG∥AC,∠1=∠2,证出∠1=∠ACD,所以EF∥CD,因此∠AEF=∠ADC=90°,即CD⊥AB.
解:CD⊥AB
∵DG⊥BC,BC⊥AC(已知)
∴∠DGB=∠_ACB__=90°(垂直定义)
∴DG∥AC,(同位角相等,两直线平行_____)
∴∠2=∠ACD__.(两直线平行,内错角相等)
∵∠1=∠2(已知)
∴∠1=∠ACD_(等量代换)
∴EF∥__CD__(同位角相等,两直线平行)
∴∠AEF=∠ADC,(_两直线平行,同位角相等__)
∵EF⊥AB,
∴∠AEF=90°
∴∠ADC=90°
即:CD⊥AB.


科目:初中数学 来源: 题型:
【题目】如图,三角形DEF是三角形ABC经过某种变换得到的图形,点A与点D、点B与点E、点C与点F分别是对应点.观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D、点B与点E、点C与点F的坐标,并说出三角形DEF是由三角形ABC经过怎样的变换得到的;
(2)若点Q(a+3,4-b)是点P(2a,2b-3)通过上述变换得到的,求a-b的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若抛物线![]() :
: ![]() (m≠0)与抛物线
(m≠0)与抛物线![]() :
: ![]() (a≠0)的开口大小相同,方向相反,且抛物线
(a≠0)的开口大小相同,方向相反,且抛物线![]() 经过
经过![]() 的顶点,我们称抛物线
的顶点,我们称抛物线![]() 为
为![]() 的“友好抛物线”.
的“友好抛物线”.
(1)若![]() 的表达式为
的表达式为![]() ,求
,求![]() 的“友好抛物线”的表达式;
的“友好抛物线”的表达式;
(2)平面上有点P (1,0),Q (3,0),抛物线![]() :
: ![]() 为
为![]() :
: ![]() 的“友好抛物线”,且抛物线
的“友好抛物线”,且抛物线![]() 的顶点在第一象限,纵坐标为2,当抛物线
的顶点在第一象限,纵坐标为2,当抛物线![]() 与线段PQ没有公共点时,求a的取值范围.
与线段PQ没有公共点时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶![]() 次,为了比较两人的成绩,制作了如下统计图表:
次,为了比较两人的成绩,制作了如下统计图表:
甲乙射击成绩统计表
平均数 | 中位数 | 方差 | 命中 | |
甲 |
|
| ||
乙 |
|
|
|
甲乙射击成绩折线图
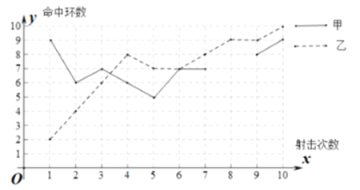
(1)请补全上述图表(请直接在统计表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,则_____胜出,理由是____________________;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y1=a1(x﹣m)2+5,点(m,25)在抛物线y2=a2x2+b2x+c2上,其中m>0.
(1)若a1=﹣1,点(1,4)在抛物线y1=a1(x﹣m)2+5上,求m的值;
(2)记O为坐标原点,抛物线y2=a2x2+b2x+c2的顶点为M,若c2=0,点A(2,0)在此抛物线上,∠OMA=90°,求点M的坐标;
(3)若y1+y2=x2+16x+13,且4a2c2﹣b22=﹣8a2,求抛物线y2=a2x2+b2x+c2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】威丽商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元?
(2)由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=4,∠BAC=120°,AD为BC边上的高,点P从点B以每秒![]() 个单位长度的速度向终点C运动,同时点Q从点C以每秒1个单位长度的速度向终点A运动,其中一个点到达终点时,两点同时停止.
个单位长度的速度向终点C运动,同时点Q从点C以每秒1个单位长度的速度向终点A运动,其中一个点到达终点时,两点同时停止.
(1)求BC的长;
(2)设△PDQ的面积为S,点P的运动时间为t秒,求S与t的函数关系式,并写出自变量的取值范围;
(3)在动点P、Q的运动过程中,是否存在PD=PQ,若存在,求出△PDQ的周长,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
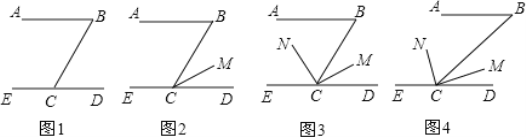
【题目】 (1)①如图1,已知AB∥CD,∠ABC=60°,可得∠BCD=_______°;
②如图2,在①的条件下,如果CM平分∠BCD,则∠BCM=_________°;
③如图3,在①、②的条件下,如果CN⊥CM,则∠BCN=___________°.
(2)、尝试解决下面问题:已知如图4,AB∥CD,∠B=40°,CN是∠BCE的平分线, CN⊥CM,求∠BCM的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com