练习册

  • 练习册
  • 试题
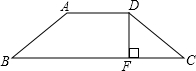    精英家教网 > 初中数学 > 题目详情
    已知直角梯形的一条对角线把梯形分成一个直角三角形和一个边长为8cm的等边三角形，则此梯形的中位线长为
     
    cm．
    分析：要求梯形的中位线，根据梯形的中位线定理，需要求得梯形的上、下底；
    结合已知条件，发现根据等边三角形和30°的直角三角形，即可求解．
    解答：精英家教网解：∵AD=AC=CD=8，∠CAD=60°，
    ∴∠BAC=90°-∠CAD=90°-60°=30°．
    在Rt△ABC中，∠BAC=30°，
    ∴BC=
    1
    2
    AC=
    1
    2
    ×8=4，
    ∴梯形中位线长是
    1
    2
    （AD+BC）=
    1
    2
    （8+4）=6．
    故答案为6．
    点评：本题利用梯形的中位线定理以及特殊角的三角函数求解．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网如图，等腰梯形ABCD中，AD=2，BC=6，高DF=2，则腰长DC=
     
    ．已知直角三角形中30°角所对的直角边长是2
    		3
    cm，则另一条直角边的长是
     
    cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图1，在直角梯形ABCD中，AD∥BC，∠B=∠A=90°，AD=a，BC=b，AB=c，
    操作示例：
    我们可以取直角梯形ABCD的非直角腰CD的中点P，过点P作PE∥AB，裁掉△PEC，并将△PEC绕点P逆时针旋转180°拼接到△PFD的位置，构成新的图形（如图2）．
    思考发现：
    判断图2中四边形ABEF的形状：
     
    ；四边形ABEF的面积是
     
    ．（用含字母的代数式表示）
    实践探究：
    类比图2的剪拼方法，请你就图3（已知：AB∥DC）画出剪拼成一个平行四边形的示意图．
    精英家教网精英家教网
    联想拓展：
    小明通过探究后发现：在一个四边形中，只要有一组对边平行，就可以剪拼成平行四边形．
    （1）如图4，在梯形ABCD中，AD∥BC，E是CD的中点，EF⊥AB于点F，AB=5，EF=4，求梯形ABCD的面积．
    （2）如图5的多边形中，AE=CD，AE∥CD，能否象上面剪切方法一样沿一条直线进行剪切，拼成一平行四边形？若能，请你在图中画出剪拼的示意图并作必要的文字说明；若不能，简要说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

     

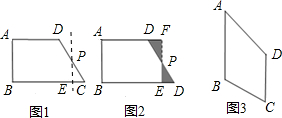
    如图1，在直角梯形ABCD中，AD∥BC，∠B=∠A=90°，AD=a，BC=b，AB=c，

    操作示例：

     我们可以取直角梯形ABCD的非直角腰CD的中点P，过点P作PE∥AB，裁掉△PEC，并将△PEC绕点P逆时针旋转180°拼接到△PFD的位置，构成新的图形（如图2）．

    思考发现：

    判断图2中四边形ABEF的形状：         ；四边形ABEF的面积是          。（用含字母的代数式表示）

    实践探究：

    类比图2的剪拼方法，请你就图3（已知：AB∥DC）画出剪拼成一个平行四边形的示意图．

    联想拓展：

    小明通过探究后发现：在一个四边形中，只要有一组对边平行，就可以剪拼成平行四边形．

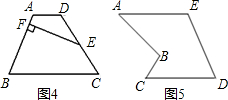
    如图4，在梯形ABCD中，AD∥BC，E是CD的中点， EF⊥AB于点F，AB=5，EF=4，求梯形ABCD的面积。

    如图5的多边形中，AE=CD，AE∥CD，能否象上面剪切方法一样沿一条直线进行剪切，拼成一平行四边形？若能，请你在图中画出剪拼的示意图并作必要的文字说明；若不能，简要说明理由．

     

    查看答案和解析>>

    科目：初中数学 来源：2012届江苏省无锡市九年级期末测试数学试卷 题型：解答题

    如图1，在直角梯形ABCD中，AD∥BC，∠B=∠A=90°，AD=a，BC=b，AB=c，

    操作示例：

     我们可以取直角梯形ABCD的非直角腰CD的中点P，过点P作PE∥AB，裁掉△PEC，并将△PEC绕点P逆时针旋转180°拼接到△PFD的位置，构成新的图形（如图2）．

    思考发现：

    判断图2中四边形ABEF的形状：          ；四边形ABEF的面积是           。（用含字母的代数式表示）

    实践探究：

    类比图2的剪拼方法，请你就图3（已知：AB∥DC）画出剪拼成一个平行四边形的示意图．

    联想拓展：

    小明通过探究后发现：在一个四边形中，只要有一组对边平行，就可以剪拼成平行四边形

    1.如图4，在梯形ABCD中，AD∥BC，E是CD的中点， EF⊥AB于点F，AB=5，EF=4，求梯形ABCD的面积。

    2.如图5的多边形中，AE=CD，AE∥CD，能否象上面剪切方法一样沿一条直线进行剪切，拼成一平行四边形？若能，请你在图中画出剪拼的示意图并作必要的文字说明；若不能，简要说明理由．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    如图，等腰梯形ABCD中，AD=2，BC=6，高DF=2，则腰长DC=________．已知直角三角形中30°角所对的直角边长是2数学公式cm，则另一条直角边的长是________cm．

    查看答案和解析>>

    同步练习册答案