
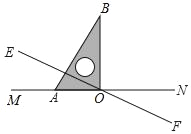
【题目】如图,直线EF与MN相交于点O,∠MOE=30°,将一直角三角尺的直角顶点与点O重合,直角边OA与MN重合,OB在∠NOE内部.操作:将三角尺绕点O以每秒5°的速度沿顺时针方向旋转一周,设运动时间为t(s).
(1)当t为何值时,直角边OB恰好平分∠NOE?此时OA是否平分∠MOE?请说明理由;
(2)若在三角尺转动的同时,直线EF也绕点O以每秒8°的速度顺时针方向旋转一周,当一方先完成旋转一周时,另一方同时停止转动.
①当t为何值时,OE平分∠AOB?
②OE能否平分∠NOB?若能请直接写出t的值;若不能,请说明理由.
【答案】(1)t=3,此时OA平分∠MOE;(2)①t=5;②t=![]() .
.
【解析】
(1)根据:角度=速度×时间进行计算,由等量关系:直角边OB恰好平分∠NOE,列出方程求解即可.
(2)①用t表示∠AOE的度数令其等于45°即可求;
②用t表示∠NOE、∠BOE的度数然后列方程解决.
(1)∵当直角边OB恰好平分∠NOE时,∠NOB= ![]() ∠NOE=
∠NOE= ![]() (180°﹣30°)=75°,
(180°﹣30°)=75°,
∴90﹣5t=75,
解得:t=3,
此时∠MOA=5°×3=15°= ![]() ∠MOE,
∠MOE,
∴此时OA平分∠MOE.
(2)①若OE平分∠AOB,
由题意得 30+8t﹣5t=90÷2,
解得 t=5;
②若OE平分∠NOB上面,
由题意得180﹣(30°+8t)= ![]() (90﹣5t),
(90﹣5t),
解得t=![]() .
.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】为迎接常熟市文明城市创建工作,某校八年一班开展了“社会主义核心价值观、未成年人基本文明礼仪规范”的知识竞赛活动,成绩分为![]() 、
、![]() 、
、![]() 、
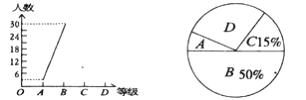
、![]() 四个等级,并将收集的数据绘制了两幅不完整的统计图.请你根据图中所给出的信息,解答下列各题:
四个等级,并将收集的数据绘制了两幅不完整的统计图.请你根据图中所给出的信息,解答下列各题:
(1)求八年一班共有多少人;
(2)补全折线统计图;
(3)在扇形统计图中等极为“![]() ”的部分所占圆心角的度数为 ;
”的部分所占圆心角的度数为 ;
(4)若等级![]() 为优秀,求该班的优秀率。
为优秀,求该班的优秀率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区准备在甲乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同.
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
甲成绩 | 9 | 4 | 7 | 4 | 6 |
乙成绩 | 7 | 5 | 7 | a | 7 |
(1)a=__,![]() =____;
=____;
(2)①分别计算甲、乙成绩的方差.
②请你从平均数和方差的角度分析,谁将被选中.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课间休息时小明拿着两根木棒玩,小华看到后要小明给他玩,小明说:“较短木棒AB长40cm,较长木棒CD长60cm,将它们的一端重合,放在同一条直线上,此时两根木棒的中点分别是点E和点F,则点E和点F间的距离是多少?你说对了我就给你玩”聪明的你请帮小华求出此时两根木棒的中点E和F间的距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小东在教学楼距地面9米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.25米处,若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)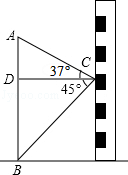
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我们学习过的数学教科书中,有一个数学活动,其具体操作过程是:
第一步:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开(如图①);
第二步:再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN(如图②).
如图②所示建立平面直角坐标系,请解答以下问题:
(Ⅰ)设直线BM的解析式为y=kx,求k的值;
(Ⅱ)若MN的延长线与矩形ABCD的边BC交于点P,设矩形的边AB=a,BC=b;
(i)若a=2,b=4,求P点的坐标;
(ii)请直接写出a、b应该满足的条件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD,点O为AD中点,点E在BD上,连接EO并延长交BC于点F,连接BE,DF.
(1)求证:四边形BEDF是平行四边形;
(2)若AB=3![]() ,AD=6,∠BAD=135°,当四边形BEDF为菱形时,求AE的长.
,AD=6,∠BAD=135°,当四边形BEDF为菱形时,求AE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com