
【题目】已知, 四边形![]() , 连接
, 连接![]() ,
,![]() ,
,![]() .
.
(1)如图![]() , 求证:
, 求证:![]() 平分
平分![]() ;
;
(2)如图![]() ,点
,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
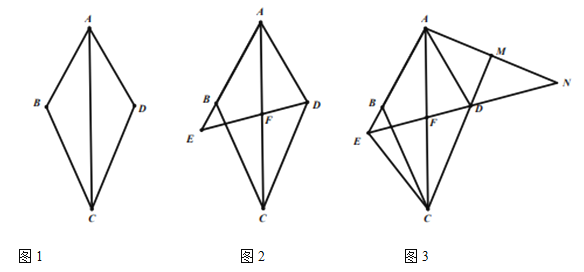
(3)如图3,在![]() 的条件下,连接
的条件下,连接![]() ,点
,点![]() 在
在![]() 延长线上,连接
延长线上,连接![]() ,延长
,延长![]() 与
与![]() 延长线交于点
延长线交于点![]() , 若
, 若![]() ,
,![]() ,
, ![]() 的面积与
的面积与![]() 的面积比为
的面积比为![]() ,
, ![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)根据“SSS”可证△ABC≌△ADC,进而可得∠BAC=∠DAC,由此即可得证;
(2)过点F作FP⊥AB,FQ⊥AD,根据角平分线的性质可得FP=FQ,进而根据S△AEF:S△ADF=AE:AD=EF:DF即可得证;
(3)先根据![]() ,
,![]() 及
及![]() 可证得
可证得![]() ,再根据△EFC和△AFN的内角和可证得
,再根据△EFC和△AFN的内角和可证得![]() ,进而可证得
,进而可证得![]() ,再根据
,再根据![]() 的面积与
的面积与![]() 的面积比为
的面积比为![]() 结合
结合![]() 可求得DN=AD=3,最后根据及求得FD的长,进而可求得FN的长.
可求得DN=AD=3,最后根据及求得FD的长,进而可求得FN的长.
(1)证明:在△ABC与△ADC中,
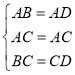
∴△ABC≌△ADC(SSS)
∴∠BAC=∠DAC,
∴![]() 平分
平分![]() ;
;
(2)证明:如图,过点F作FP⊥AB,FQ⊥AD,垂足分别为点P、Q,
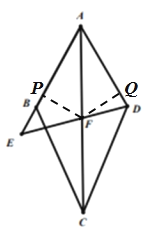
∵![]() 平分
平分![]() ,FP⊥AB,FQ⊥AD,
,FP⊥AB,FQ⊥AD,
∴FP=FQ,
∴S△AEF:S△ADF=![]() AE·FP:
AE·FP:![]() AD·FQ= AE:AD,
AD·FQ= AE:AD,
设点A到DE的距离为h,
则S△AEF:S△ADF=![]() EF·h:
EF·h:![]() FD·h=EF:FD,
FD·h=EF:FD,
∴AE:AD=EF:FD;
(3)解:∵![]() ,
,
∴![]() ,
,
∵![]()
∴![]() ,
,
∵![]() ,
,
∴![]()
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
且![]() ,
,
∴![]()
∴![]()
∴![]()
∵![]() 的面积与
的面积与![]() 的面积比为
的面积比为![]()
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
∵![]() ,
,![]()
∴![]()
![]()
![]() ,
,
∴![]()
![]()
![]() .
.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】在一条直线上依次有A,B,C三个海岛,某海巡船从A岛出发沿直线匀速经B岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(时)后,与B港的距离为y(海里),y与x之间的函数图象如图所示.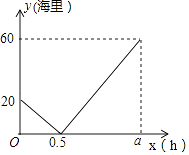
(1)A,C两港口间的距离为海里,a=
(2)求y与x之间的函数关系式.
(3)在B岛上有一个不间断发射信号的信号发射台,发射的信号覆盖半径为8海里的圆形区域,求该海巡船鞥接受到该信号的时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,等边三角形ABC放置在平面直角坐标系中,已知A(0,0)、B(6,0),反比例函数的图象经过点C.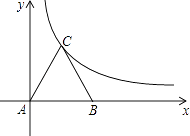
(1)求点C的坐标及反比例函数的解析式.
(2)将等边△ABC向上平移n个单位,使点B恰好落在双曲线上,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣2,0)、B(4,0)两点,与y轴交于点C.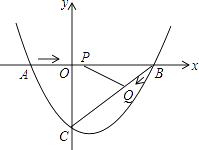
(1)求抛物线的解析式;
(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?
(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S△CBK:S△PBQ=5:2,求K点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点A表示3街与5大道的十字路口,点B表示5街与3大道的十字路口,如果用(3,5)→(4,5)→(5,5)→(5,4)→(5,3)表示由A到B的一条路径,那么你能用同样的方法写出由A到B的其他几条路径吗?请至少给出3种不同的路径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间关系的图像如图所示.根据图像解答下列问题:
(1)谁先出发?先出发多少时间?谁先到达终点?先到多少时间?
(2)分别求出甲、乙两人的行驶速度;
(3)在什么时间段内,两人均行驶在途中?(不包括起点和终点)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要得到△ABD≌△ACE,从下列条件中补选一个,则错误的是( )

A.AB=AC B.DB=EC C.∠ADB=∠AEC D.∠B=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家快餐店销售![]() 三种套餐,其中
三种套餐,其中![]() 套餐包含一荤两素,
套餐包含一荤两素,![]() 套餐包含两荤一素,
套餐包含两荤一素,![]() 套餐包含两荤两素,每份套餐中一荤的成本相同,一素的成本也相同,已知一份
套餐包含两荤两素,每份套餐中一荤的成本相同,一素的成本也相同,已知一份![]() 套餐的售价是一份
套餐的售价是一份![]() 套餐和一份
套餐和一份![]() 套餐售价之和的
套餐售价之和的![]() 一天下来,店长发现
一天下来,店长发现![]() 套餐和
套餐和![]() 套餐的销量相同,且
套餐的销量相同,且![]() 套餐的利润和是
套餐的利润和是![]() 套餐利润的两倍,当天的总利润率是
套餐利润的两倍,当天的总利润率是![]() .第二天店内搞活动,
.第二天店内搞活动,![]() 套餐的售价打五折,
套餐的售价打五折,![]() 套餐的售价均不变,当
套餐的售价均不变,当![]() 三种套餐的销量相同时,总利润率为________.
三种套餐的销量相同时,总利润率为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com