
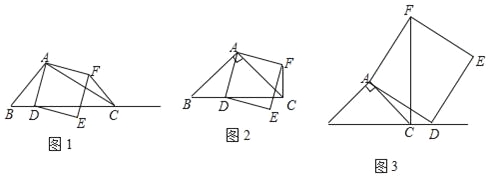
【题目】如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,联结AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图2,将△ABD绕A点逆时针旋转90°,所得到的三角形为 ,线段CF、BD所在直线的位置关系为 ,线段CF、BD的数量关系为 ;
②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F不重合),并说明理由.
【答案】(1)①△ACF,垂直,相等
②结论是否仍然成立,理由见解析
(2)当∠ACB=45°时,CF⊥BC,理由见解析
【解析】
试题分析:解题的关键是过点A作AG⊥AC交CB的延长线于点G,构造全等三角形.(1)①当点D在线段BC上时,根据等腰直角三角形的性质以及旋转的性质,即可得出CF=BD,BD⊥CF;②当点D在BC的延长线上时,①的结论仍成立.由正方形ADEF的性质可推出△DAB≌△FAC,所以CF=BD,∠ACF=∠ABD,结合∠BAC=90°,AB=AC,得到∠BCF=∠ACB+∠ACF=90°,即CF⊥BD;
(2)当∠ACB=45°时,过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°,可推出∠ACB=∠AGC,所以AC=AG,由(1)①中的方法可得CF⊥BD.
解:(1)①如图2所示,将△ABD绕A点逆时针旋转90°,所得到△ACF,则
由旋转的性质可得:∠ACF=∠B,CF=BD,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°=∠ACF,
∴∠BCF=90°,即BD⊥CF;
故答案为:△ACF,垂直,相等;
②如图3所示,当点D在BC的延长线上时,①中的结论仍成立.
证明:由正方形ADEF得,AD=AF,∠DAF=90°.
∵∠BAC=90°
∴∠DAF=∠BAC,
∴∠DAB=∠FAC,
又∵AB=AC,
∴△DAB≌△FAC(SAS),
∴CF=BD,∠ACF=∠ABD.
∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
∴∠ACF=45°,
∴∠BCF=∠ACB+∠ACF=90°,即 CF⊥BD;
(2)如图4所示,当∠ACB=45°时,CF⊥BD.
理由:过点A作AG⊥AC交CB或CB的延长线于点G,则∠GAC=90°,
∵∠ACB=45°,∠AGC=90°﹣∠ACB=45°,
∴∠ACB=∠AGC,
∴AC=AG,
又∵∠DAG=∠FAC(同角的余角相等),AD=AF,
∴△GAD≌△CAF(SAS),
∴∠ACF=∠AGC=45°,
∴∠BCF=∠ACB+∠ACF=45°+45°=90°,即CF⊥BC.



科目:初中数学 来源: 题型:
【题目】“鼓楼e学校一停课不停学在线课堂”在此次疫情期间为全国师生提供鼓楼教育的“云服务”,课程日均访问量达1200000,用科学记数法表示1200000是( )
A.0.12×106B.1.2×107C.1.2×106D.12×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,线段A′B′是由线段AB经过平移得到的,已知点A(﹣2,1)的对应点为A′(3,﹣1),点B的对应点为B′(4,0),则点B的坐标为( )
A.(9,﹣2)
B.(﹣1,﹣2)
C.(9,2)
D.(﹣1,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
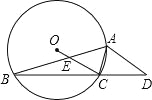
【题目】如图所示,⊙O的内接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延长线于D点,OC交AB于E点.
(1)求∠D的度数;
(2)求证:AC2=ADCE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A的坐标为(3,-2),则点A向右平移3个单位后的坐标为( )
A. (0,-2) B. (6,-2) C. (3,1) D. (3,-5)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com