
【题目】如图,在菱形ABCD中,对角线AC与BD相交于点O,MN过点O且与边AD、BC分别交于点M和点N.
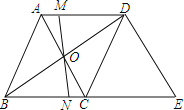
(1)请你判断OM与ON的数量关系,并说明理由;
(2)过点D作DE∥AC交BC的延长线于E,当AB=5,AC=6时,求△BDE的周长.
【答案】(1)OM=ON.(2)24.
【解析】
试题分析:(1)根据四边形ABCD是菱形,判断出AD∥BC,AO=OC,即可推得OM=ON.
(2)首先根据四边形ABCD是菱形,判断出AC⊥BD,AD=BC=AB=5,进而求出BO、BD的值是多少;然后根据DE∥AC,AD∥CE,判断出四边形ACED是平行四边形,求出DE=AC=6,即可求出△BDE的周长是多少.
解:(1)∵四边形ABCD是菱形,
∴AD∥BC,AO=OC,
∴![]() =
=![]() =1,
=1,
∴OM=ON.
(2)∵四边形ABCD是菱形,
∴AC⊥BD,AD=BC=AB=5,
∴BO=![]() =4,
=4,
∴BD=2BO=8,
∵DE∥AC,AD∥CE,
∴四边形ACED是平行四边形,
∴DE=AC=6,
∴△BDE的周长是:
BD+DE+BE
=BD+AC+(BC+CE)
=8+6+(5+5)
=24
即△BDE的周长是24.



科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
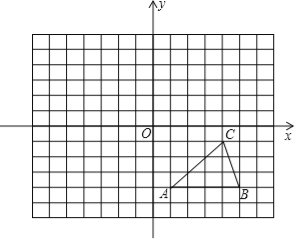
(1)把△ABC向上平移5个单位后得到对应的△A1B1C1,画出△A1B1C1,并写出C1的坐标;
(2)以原点O为对称中心,再画出与△A1B1C1关于原点O对称的△A2B2C2,并写出点C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(8,8),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.
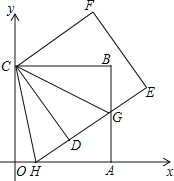
(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;判断线段HG、OH、BG的数量关系,并说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BO、CO分别是∠ABC、∠ACB的角平分线,求:

(1)若∠A=50°,求∠BOC的度数.
(2)在其他条件不变的情况下,若∠A=n°,则∠A与∠BOC之间有怎样的数量关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)x(﹣x2)x3;
(2)(xy)5÷(xy)3
(3)a5(﹣a)3+(﹣2a2)4;
(4)|﹣2|+(﹣2)2+(7﹣π)0﹣(![]() )﹣1.
)﹣1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列条件,能判定一个三角形是直角三角形的是( )
A.三条边的边长之比是1:2:3
B.三个内角的度数之比是1:1:2
C.三条边的边长分别是![]() ,
,![]() ,
,![]()
D.三条边的边长分别是12,15,20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com