
分析 根据(a+b)(a-b)=a2-b2,可得出$\sqrt{53-{x}^{2}}$+$\sqrt{13-{x}^{2}}$=[($\sqrt{53-{x}^{2}}$)2-($\sqrt{13-{x}^{2}}$)2]÷($\sqrt{53-{x}^{2}}$-$\sqrt{13-{x}^{2}}$),然后进行求解即可.
解答 解:∵$\sqrt{53-{x}^{2}}$-$\sqrt{13-{x}^{2}}$=2,
∴$\sqrt{53-{x}^{2}}$+$\sqrt{13-{x}^{2}}$
=[($\sqrt{53-{x}^{2}}$)2-($\sqrt{13-{x}^{2}}$)2]÷($\sqrt{53-{x}^{2}}$-$\sqrt{13-{x}^{2}}$)
=[53-x2-13+x2]÷2
=40÷2
=20.
故答案为:20.
点评 本题考查了二次根式的加减法,解答本题的关键在于根据(a+b)(a-b)=a2-b2得出$\sqrt{53-{x}^{2}}$+$\sqrt{13-{x}^{2}}$=[($\sqrt{53-{x}^{2}}$)2-($\sqrt{13-{x}^{2}}$)2]÷($\sqrt{53-{x}^{2}}$-$\sqrt{13-{x}^{2}}$),然后进行求解.


科目:初中数学 来源: 题型:解答题
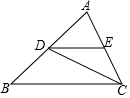 如图,△ABC中,AB=4,点D在AB边上移动(不与A,B重合),DE∥BC,交AC于点E,连接CD,设S△ABC=S,S△DCE=S1.
如图,△ABC中,AB=4,点D在AB边上移动(不与A,B重合),DE∥BC,交AC于点E,连接CD,设S△ABC=S,S△DCE=S1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果a=b,那么a-c=b-c | B. | 如果$\frac{a}{c}=\frac{b}{c}$,那么a=b | ||
| C. | 如果ac2=bc2,那么a=b | D. | 如果a(c2+1)=b(c2+1),那么a=b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
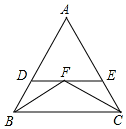 如图,在△ABC中,∠ABC的平分线BF与∠ACB的平分线CF相交于F,过点F作DE∥BC,交直线AB于点D,交直线AC于点E.那么BD,CE,DE之间存在什么数量关系?并证明这种关系.
如图,在△ABC中,∠ABC的平分线BF与∠ACB的平分线CF相交于F,过点F作DE∥BC,交直线AB于点D,交直线AC于点E.那么BD,CE,DE之间存在什么数量关系?并证明这种关系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com