


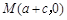
 1分
1分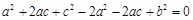 ∴
∴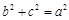 . 1分
. 1分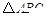 为直角三角形且∠A=90° 1分
为直角三角形且∠A=90° 1分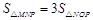
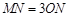 即
即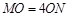 1分
1分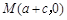 ∴
∴
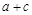 ,
,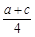 是方程x2-2ax+b2=0的两根
是方程x2-2ax+b2=0的两根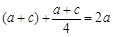 ∴
∴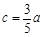 1分
1分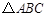 中,∠A=90°
中,∠A=90°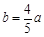 ∴sinB=
∴sinB=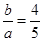 1分
1分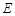 则NE=EM DN=DM
则NE=EM DN=DM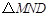 为等腰直角三角形,只须ED=
为等腰直角三角形,只须ED=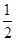 MN=EM
MN=EM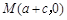
 ∴
∴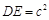
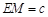
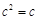 又c>0,∴c=1 1分
又c>0,∴c=1 1分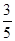 a b=
a b=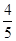 a ∴a=
a ∴a=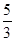 b=
b=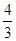 1分
1分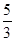 ,b=
,b=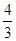 ,c=1时,
,c=1时,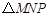 为等腰直角三角形 1分
为等腰直角三角形 1分


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com