
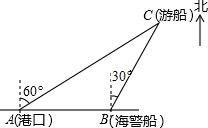
 一艘观光游船从港口A以北偏东60°的方向出港观光,航行60海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东30°方向,马上以40海里每小时的速度前往救援,海警船到达事故船C处所需的时间大约为$\frac{\sqrt{3}}{2}$小时(用根号表示).
一艘观光游船从港口A以北偏东60°的方向出港观光,航行60海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东30°方向,马上以40海里每小时的速度前往救援,海警船到达事故船C处所需的时间大约为$\frac{\sqrt{3}}{2}$小时(用根号表示). 分析 过点C作CD⊥AB交AB延长线于D.先解Rt△ACD得出CD=$\frac{1}{2}$AC=40海里,再解Rt△CBD中,得出BC=$\frac{CD}{sin∠CBD}$=$\frac{30}{\frac{\sqrt{3}}{2}}$=20$\sqrt{3}$(海里),然后根据时间=路程÷速度即可求出海警船到大事故船C处所需的时间.
解答 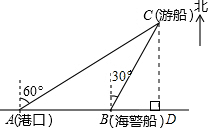 解:如图,过点C作CD⊥AB交AB延长线于D.
解:如图,过点C作CD⊥AB交AB延长线于D.
在Rt△ACD中,
∵∠ADC=90°,∠CAD=30°,AC=60海里,
∴CD=$\frac{1}{2}$AC=30海里.
在Rt△CBD中,
∵∠CDB=90°,∠CBD=90°-37°=53°,
∴BC=$\frac{CD}{sin∠CBD}$=$\frac{30}{\frac{\sqrt{3}}{2}}$=20$\sqrt{3}$(海里),
∴海警船到大事故船C处所需的时间大约为:20$\sqrt{3}$÷40=$\frac{\sqrt{3}}{2}$(小时).
故答案为$\frac{\sqrt{3}}{2}$.
点评 本题考查了解直角三角形的应用-方向角问题,难度适中,作出辅助线构造直角三角形是解题的关键


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:解答题
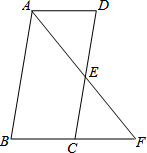 如图,在?ABCD中,点E是DC的中点,连接AE,并延长交BC的延长线于点F.
如图,在?ABCD中,点E是DC的中点,连接AE,并延长交BC的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
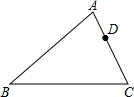 如图,在△ABC中,AB=8,AC=6,点D在AC上,且AD=2,如果要在AB上找一点E,使△ADE与△ABC相似,则AE的长为( )
如图,在△ABC中,AB=8,AC=6,点D在AC上,且AD=2,如果要在AB上找一点E,使△ADE与△ABC相似,则AE的长为( )| A. | $\frac{8}{3}$ | B. | $\frac{3}{2}$ | C. | 3 | D. | $\frac{8}{3}$或$\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com