
【题目】如图,在平面直角坐标系中,A(﹣1,4),B(﹣4,0),C(﹣1,0).

(1)△A1B1C1与△ABC关于原点O对称,画出△A1B1C1并写出点A1的坐标;
(2)△A2B2C2是△ABC绕原点O顺时针旋转90°得到的,画出△A2B2C2并写出点A2的坐标;
(3)连接OA、OA2,在△ABC绕原点O顺时针旋转90°得到的△A2B2C2的过程中,计算线段OA变换到OA2过程中扫过区域的面积是多少?(直接写出答案)
科目:初中数学 来源: 题型:
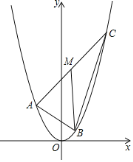
【题目】如图,A、B、C三点均在二次函数y=x2的图象上,M为线段AC的中点,BM∥y轴,且MB=2.设A、C两点的横坐标分别为t1、t2(t2>t1),则t2﹣t1的值为( )
A.3B.2![]() C.2
C.2![]() D.2
D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
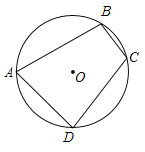
【题目】如图,已知⊙O的半径为4,四边形ABCD为⊙O的内接四边形,且AB=4![]() ,AD=4
,AD=4![]() ,则∠BCD的度数为( )
,则∠BCD的度数为( )
A.105°B.115°C.120°D.135°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近期猪肉价格不断走高,引起了民众与政府的高度关注,当市场猪肉的平均价格每千克达到一定的单价时,政府将投入储备猪肉以平抑猪肉价格.据统计:从今年年初至7月20日,猪肉价格不断走高,7月20日比年初价格上涨了60%.某市民于某超市今年7月20日购买2.5千克猪肉花100元钱.
(1)问:那么今年年初猪肉的价格为每千克多少元?
(2)某超市将进货价为每千克30元的猪肉,按7月20日价格出售,平均一天能销售出100千克,经调查表明:猪肉的售价每千克下降1元,其日销售量就增加20千克,超市为了实现销售猪肉每天有1120元的销售利润,为了尽可能让顾客优惠应该每千克定价为多少元?
(3)7月21日,某市决定投入储备猪肉并规定其在原销售价的基础上下调a%出售,某超市按规定价出售一批储备猪肉,该超市在非储备猪肉的价格不变情况下,该天的两种猪肉总销量比7月20日增加了a%,且储备猪肉的销量占总销量的![]() ,两种猪肉销售的总金额比7月20日提高了
,两种猪肉销售的总金额比7月20日提高了![]() a%,求a的值.
a%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
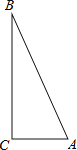
【题目】实践:如图△ABC是直角三角形,∠ACB=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
(1)作∠BAC的平分线,交BC于点O.
(2)以O为圆心,OC为半径作圆.
综合运用:在你所作的图中,
(1)AB与⊙O的位置关系是_____ .(直接写出答案)
(2)若AC=5,BC=12,求⊙O 的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角三角形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 上的一点,以点
上的一点,以点![]() 为圆心,
为圆心,![]() 为半径的圆弧与
为半径的圆弧与![]() 相切于点
相切于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
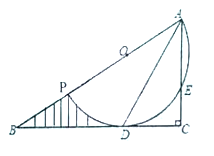
(1)求证:![]() 平分
平分![]() ;
;
(2)若![]() ,求圆弧的半径;
,求圆弧的半径;
(3)在![]() 的情况下,若
的情况下,若![]() ,求阴影部分的面积(结果保留
,求阴影部分的面积(结果保留![]() 和根号)
和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某校为了让学生的课余生活丰富多彩,开展了以下课外活动:
代号 | 活动类型 |
A | 经典诵读与写作 |
B | 数学兴趣与培优 |
C | 英语阅读与写作 |
D | 艺体类 |
E | 其他 |
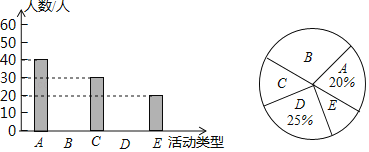
为了解学生的选择情况,现从该校随机抽取了部分学生进行问卷调查(参与问卷调查的每名学生只能选择其中一项),并根据调查得到的数据绘制了如图所示的两幅不完整的统计图.请根据统计图提供的信息回答下列问题(要求写出简要的解答过程).
(1)此次共调查了 名学生.
(2)将条形统计图补充完整.
(3)“数学兴趣与培优”所在扇形的圆心角的度数为 .
(4)若该校共有2000名学生,请估计该校喜欢A、B、C三类活动的学生共有多少人?
(5)学校将从喜欢“A”类活动的学生中选取4位同学(其中女生2名,男生2名)参加校园“金话筒”朗诵初赛,并最终确定两名同学参加决赛,请用列表或画树状图的方法,求出刚好一男一女参加决赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,点P在AD上,AB=2,AP=1.直角尺的直角顶点放在点P处,直角尺的两边分别交AB、BC于点E、F,连接EF(如图1).
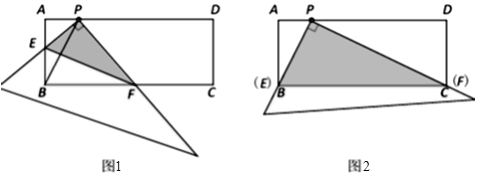
(1)当点E与点B重合时,点F恰好与点C重合(如图2).
①求证:△APB∽△DCP;
②求PC、BC的长.
(2)探究:将直角尺从图2中的位置开始,绕点P顺时针旋转,当点E和点A重合时停止.在这个过程中(图1是该过程的某个时刻),观察、猜想并解答:
① tan∠PEF的值是否发生变化?请说明理由.
② 设AE=x,当△PBF是等腰三角形时,请直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠B=600,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
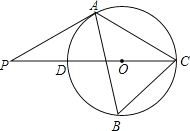
(1)求证:PA是⊙O的切线;
(2)若PD=![]() ,求⊙O的直径.
,求⊙O的直径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com