
【题目】已知一次函数y= ![]() 过点A(2,4),B(0,3)、题目中的矩形部分是一段因墨水污染而无法辨认的文字.
过点A(2,4),B(0,3)、题目中的矩形部分是一段因墨水污染而无法辨认的文字.
(1)根据现有的信息,请求出题中的一次函数的解析式.
(2)根据关系式画出这个函数图象.
(3)过点B能不能画出一直线BC将△ABO(O为坐标原点)分成面积比为1:2的两部分?如能,可以画出几条,并求出其中一条直线所对应的函数关系式,其它的直接写出函数关系式;若不能,说明理由.
【答案】(1) y=0.5x+3.(2)作图见解析;(3)y=-2.5x+3或y=-0.25x+3.
【解析】试题分析:(1)设一次函数的解析式是y=kx+b,把A(0,3)、B(2,4)代入得出方程组,求出方程组的解即可;
(2)过A、B作直线即可;
(3)根据面积得出C、C′点,求出直线AO的解析式,根据A的坐标求出C和C′的坐标,设直线BC的解析式,把B、C(或)C′的坐标代入求出即可.
试题解析:(1)解:设一次函数的解析式是y=kx+b,
∵把A(0,3)、B(2,4)代入得:
![]() ,解得:k=0.5,b=3,
,解得:k=0.5,b=3,
∴一次函数的解析式是y=0.5x+3.
(2)解:如图.
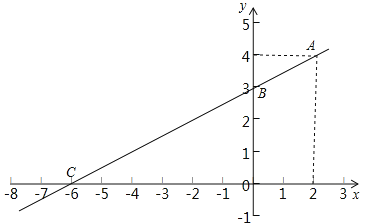
(3)解:能,有两条,如图:
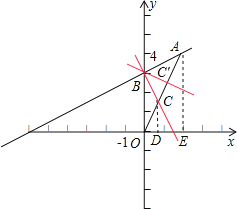
直线BC和BC′都符合题意,
OC=CC′=AC′,
则C的纵坐标是![]() ×4=
×4=![]() ,
,
C′的纵坐标是![]() ×4=
×4= ![]() ,
,
设直线OA的解析式是y=kx,
把A(2,4)代入得:k=2,
∴y=2x,
把C、C′的纵坐标代入得出C的横坐标是![]() ,C′的横坐标是
,C′的横坐标是![]() ,
,
∴C(![]() ,
,![]() ),C′(
),C′(![]() ,
,![]() ),
),
设直线BC的解析式是y=kx+3,
把C的坐标代入得:k=-2.5,
∴直线BC的解析式是y=-2.5x+3,
同理求出直线BC′的解析式是y=-0.25x+3,
即过点B能画出直线BC将△ABO(O为坐标原点)分成面积比为1:2的两部分,可以画出2条,直线所对应的函数关系式是y=-2.5x+3或y=-0.25x+3.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
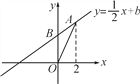
【题目】已知平面直角坐标系xOy(如图),直线 y=![]() x+b经过第一、二、三象限,与y轴交于点B,点A(2,t)在直线y=
x+b经过第一、二、三象限,与y轴交于点B,点A(2,t)在直线y=![]() x+b上,连结AO,△AOB的面积等于1.
x+b上,连结AO,△AOB的面积等于1.
(1)求b的值;
(2)如果反比例函数y=![]() (k是常量,k≠0)的图象经过点A,求这个反比例函数的表达式.
(k是常量,k≠0)的图象经过点A,求这个反比例函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D在反比例函数y= ![]() 的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=
的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC= ![]() .
.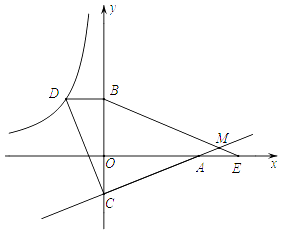
(1)求反比例函数y= ![]() 和直线y=kx+b的解析式;
和直线y=kx+b的解析式;
(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA与点M,求∠BMC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A为函数y= ![]() (x>0)图象上一点,连结OA,交函数y=
(x>0)图象上一点,连结OA,交函数y= ![]() (x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为 .
(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为 . 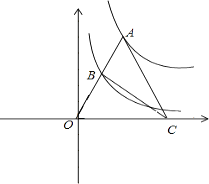
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一列有理数-1,2,-3,4,-5,6,…如图排序,根据图中的排列规律可知,“峰1”中峰顶的位置(C的位置)是有理数4,那么“峰4”中C的位置是有理数________,有理数“2018”应排在A,B,C,D,E中的________位置.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的三边长,且满足2a4+2b4+c4=2a2c2+2b2c2,则△ABC是( )
A. 等腰三角形 B. 等腰直角三角形
C. 直角三角形 D. 等腰三角形或直角三角形
【答案】B
【解析】解析:∵2a4+2b4+c4=2a2c2+2b2c2,∴4a4-4a2c2+c4+4b4-4b2c2+c4=0,
∴(2a2-c2)2+(2b2-c2)2=0,∴2a2-c2=0,2b2-c2=0,
∴c=2a,c=2b,
∴a=b,且a2+b2=c2,
∴△ABC为等腰直角三角形.
故选B.
【题型】单选题
【结束】
11
【题目】将图1中阴影部分的小长方形变换到图2的位置,你能根据两个图形的面积关系得到的数学公式是_____.
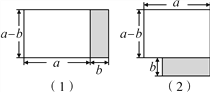
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥EF,BC⊥CD于点C,∠ABC=30°,∠DEF=45°,则∠CDE等于( )

A. 105° B. 75° C. 135° D. 115°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 △ABC 中,∠C=90°,DB⊥BC 于点 ,分别以点 D 和点 为圆心,以大于![]() 的长为半径作弧,两弧相交于点 E 和点 ,作直线 EF,延长 AB 于点 ,连接 DG,下面是说明 ∠A=∠D 的说理过程,请把下面的说理过程补充完整:
的长为半径作弧,两弧相交于点 E 和点 ,作直线 EF,延长 AB 于点 ,连接 DG,下面是说明 ∠A=∠D 的说理过程,请把下面的说理过程补充完整:
因为 DB⊥BC(已知),
所以 ∠DBC=90°( ) .
因为 ∠C=90°(已知),
所以 ∠DBC=∠C(等量代换),
所以 DB∥AC ( ) ,
所以 (两直线平行,同位角相等);
由作图法可知:直线 EF 是线段 DB 的 ( ) ,
所以 GD=GB,线段 (上的点到线段两端点的距离相等),
所以 ( ) ,因为 ∠A=∠1(已知),
所以 ∠A=∠D(等量代换).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com