
【题目】如图,在△ABC中,∠ABC=60°,AC=2AB,AD平分∠BAC交BC于点D,延长DB至点F,使BF=BD连接AF.
(1)求证:AF=CD.
(2)若CE平分∠ACB交AB于点E,试猜想AC,AF,AE三条线段之间的数量关系,并证明你的猜想.

【答案】(1)证明见解析;(2) AC=AF+AE,证明见解析
【解析】
(1)取AC的中点E,连接DE,根据题目已知条件可以证得△ABD≌△AED,再利用全等三角形的性质,可以证得△AFB≌△CDE,即可得出结论;
(2) 在AC上取一点M,使得AM=AE,根据AD是∠BAC的角平分线,CE是∠ACB的角平分线,可以得出∠AOE=60°,根据条件可以证得△AEO≌△AMO,利用全等三角形的性质可以证得△COD≌△COM,故可以得出结果.
(1)证明:如图所示,取AC的中点E,连接DE,
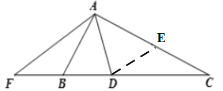
∵AC=2AB,
∴AB=AE=EC,
∵AD是∠BAC的角平分线,
∴∠BAD=∠DAC,
在△ABD和△AED中
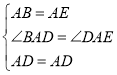
∴△ABD≌△AED,
∴∠ABD=∠AED,DB=DE,
∴∠ABF=∠DEC,
∵FB=BD,
∴FB=DE,
在△AFB和△CDE中
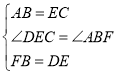
△AFB≌△CDE,
∴AF=DC.
(2)猜想:AC=AF+AE,
证明:如图所示,在AC上取一点M,使得AM=AE
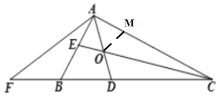
∵AD是∠BAC的角平分线,CE是∠ACB的角平分线,
∴∠BAD=∠DAC,∠ACE=∠ECB,
∵∠ABC=60°,
∴∠BAC+∠ACB=120°,
∴∠ACE+∠OAC=60°,
∴∠AOC=120°,
∴∠AOE=60°,
在△AEO和△AMO中
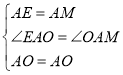
∴△AEO≌△AMO,
∴∠AOE=∠AOM=60°,
∴∠MOC=60°,
∵∠AOE=∠DOC,
∴∠DOC=60°,
在△COD和△COM中
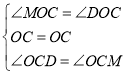
∴△COD≌△COM,
∴CM=CD,
由题(1)知CD=AF,
∴AF=CM,
∴AC=AM+MC=AE+AF.


科目:初中数学 来源: 题型:
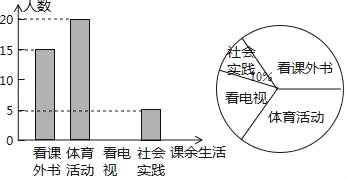
【题目】为了解某中学学生课余生活情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计.现从该校随机抽取n名学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名学生只能选择其中一项).并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图.由图中提供的信息,解答下列问题:
(1)求n的值;
(2)若该校学生共有1200人,试估计该校喜爱看电视的学生人数;
(3)若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名学生,求恰好抽到2名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习了三角形全等的判定方法(即SSS,SAS,ASA,AAS)和直角三角形全等的判定方法(即HL)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
(初步思考)
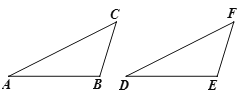
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后对∠B进行分类,可以分为“∠B是直角、钝角、锐角”三种情况进行探究.
(深入探究)
第一种情况:当∠B为锐角时,△ABC和△DEF不一定全等.
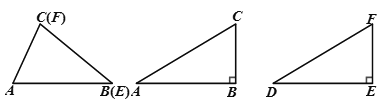
(1)如图,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角,请你用尺规在图中确定点D,使△DEF和△ABC不全等(不写作法,保留作图痕迹);
第二种情况:当∠B为直角时,△ABC≌△DEF.
(2)如图,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据____,可以知道Rt△ABC≌Rt△DEF.
第三种情况:当∠B为钝角时,△ABC≌△DEF.
(3)如图,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是钝角,求证:△ABC≌△DEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
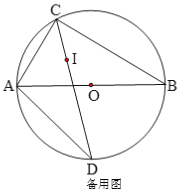
【题目】如图,⊙![]() 是Rt△ABC的外接圆,∠ACB=90°,点I是△ABC的内心,CI的延长线交⊙O于点D,连接AD.
是Rt△ABC的外接圆,∠ACB=90°,点I是△ABC的内心,CI的延长线交⊙O于点D,连接AD.
(1)求证:DA=DI.
(2)若AB=10,AC=6,求AD、CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
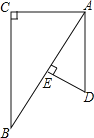
【题目】如图,已知△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,那么添加下列一个条件后,仍无法判定△ABC∽△DAE的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
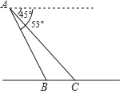
【题目】小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为53°和45°,已知大桥BC与地面在同一水平面上,其长度为75m,请求出热气球离地面的高度.(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com