
【题目】在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到AE,连结EC.如果AB=AC,∠BAC=90°.
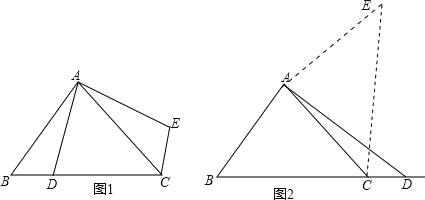
①当点D在线段BC上时(与点B不重合),如图1,请你判断线段CE、BD之间的位置和数量关系(直接写出结论);
②当点D在线段BC的延长线上时,请你在图2画出图形,判断①中的结论是否仍然成立,并证明你的判断.

【答案】(1)线段CE,BD之间的位置关系和数量关系为:CE=BD,CE⊥BD.(2)线段CE,BD之间的位置关系和数量关系为:CE=BD,CE⊥BD.
【解析】
试题分析:①线段AD绕点A逆时针旋转90°得到AE,根据旋转的性质得到AD=AE,∠BAD=∠CAE,得到△BAD≌△CAE,CE=BD,∠ACE=∠B,得到∠BCE=∠BCA+∠ACE=90°,于是有CE=BD,CE⊥BD.
②结论仍然成立.证明的方法与(1)类似.
试题解析:①结论:CE=BD,CE⊥BD.理由如下:
如图1中,∵AB=AC,∠BAC=90°,∴线段AD绕点A逆时针旋转90°得到AE,
∴AD=AE,∵∠BAC=∠DAE=90°,∴∠BAD=∠CAE,∵AB=AC,AD=AE,
∴△BAD≌△CAE,∴CE=BD,∠ACE=∠B,
∴∠BCE=∠BCA+∠ACE=90°,
∴线段CE,BD之间的位置关系和数量关系为:CE=BD,CE⊥BD.
②结论仍然成立.理由如下:如图2中,∵线段AD绕点A逆时针旋转90°得到AE,
∴AE=AD,∠DAE=90°,∵AB=AC,∠BAC=90°,∴∠CAE=∠BAD,
∴△ACE≌△ABD,∴CE=BD,∠ACE=∠B,∴∠BCE=90°,
所以线段CE,BD之间的位置关系和数量关系为:CE=BD,CE⊥BD.


科目:初中数学 来源: 题型:
【题目】如图,△ABC内有一点D,且DA=DB=DC.若∠DAB=20°,∠DAC=30°,则∠BDC的度数为( )

A. 100° B. 80° C. 70° D. 50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”,自行车正逐渐成为人们喜爱的交通工具,某运动商城的自行车销售量自2017年起逐月增加,据统计,该商城1月份销售自行车64辆,3月份销售了100辆,若该商城自2017起每个月自行车销量的月平均增长率相同,求月平均增长率.若设月平均增长率为x,由题意可得方程:________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式计算正确的是( )
A.2a2+3a2=5a4
B.(﹣2ab)3=﹣6ab3
C.(3a+b)(3a﹣b)=9a2﹣b2
D.a3(﹣2a)=﹣2a3
查看答案和解析>>
科目:初中数学 来源: 题型:
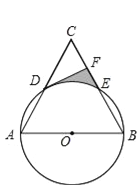
【题目】已知:如图,以等边三角形ABC一边AB为直径的⊙O与边AC、BC分别交于点D、E,过点D作DF⊥BC,垂足为F.
(1)求证:DF为⊙O的切线;
(2)若等边三角形ABC的边长为4,求DF的长;
(3)写出求图中阴影部分的面积的思路.(不求计算结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点分别为A(﹣4,3),B(﹣6,1),C(﹣1,1),将△ABC绕着原点O顺时针旋转180°后得到△A1B1C1 , 则点B的对应点B1的坐标是( )
A.(1,﹣1)
B.(4,﹣3)
C.(﹣1,﹣1)
D.(6,﹣1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com