
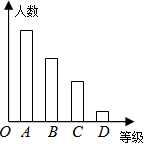
 某校对九年级学生进行“综合素质”评价,评价的结果为A(优)、B(良好)、C(合格)、D(不合格)四个等级.现从中抽测了若干名学生的“综合素质”等级作为样本进行数据处理,并作出图所示的统计图,已知图中从左到右的四个长方形的高的比为:14:9:6:1,评价结果为D等级的有2人,请你回答以下问题:
某校对九年级学生进行“综合素质”评价,评价的结果为A(优)、B(良好)、C(合格)、D(不合格)四个等级.现从中抽测了若干名学生的“综合素质”等级作为样本进行数据处理,并作出图所示的统计图,已知图中从左到右的四个长方形的高的比为:14:9:6:1,评价结果为D等级的有2人,请你回答以下问题:分析 ①图中从左到右的四个长方形的高的比为:14:9:6:1,可知比份总和为30,根据评价结果为D等级的有2人可求出总数;
②根据图中频数与频率的关系求
③圆心角为360度,按比份求扇形度数.
④先求出样本中报考示范性高中的频率再乘300.
解答 解:①2÷$\frac{1}{30}$=2×30=60人,
∴抽测了60人;
②∵9÷30=0.3,
∴样本中B等级的频率是0.3,
故答案为:60,0.3;
③D等级在扇形统计图中所占的圆心角为:$\frac{1}{30}$×360°=12°;
故答案为:12;
④$\frac{14+9}{30}$×300=230名,
∴估计该校大约有230名学生可以报考示范性高中.
点评 此题主要考查了条形统计图以及利用样本估计总体等知识,正确掌握利用样本估计总体的方法是解题关键.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
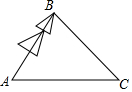 如图,为了对一颗倾斜的古杉树AB进行保护,需测量其长度:在地面上选取一点C,测得∠ACB=45°,AC=24m,∠BAC=66.5°,(参考数据:$\sqrt{2}$≈1.414,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30).则这颗古杉树AB的长约为( )
如图,为了对一颗倾斜的古杉树AB进行保护,需测量其长度:在地面上选取一点C,测得∠ACB=45°,AC=24m,∠BAC=66.5°,(参考数据:$\sqrt{2}$≈1.414,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30).则这颗古杉树AB的长约为( )| A. | 7.27 | B. | 16.70 | C. | 17.70 | D. | 18.18 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
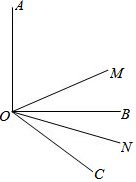 (1)如图,已知∠AOB=90°,∠BOC=40°,OM平分∠AOC,ON平分∠BOC.求∠MON的度数.
(1)如图,已知∠AOB=90°,∠BOC=40°,OM平分∠AOC,ON平分∠BOC.求∠MON的度数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com