
【题目】某文具商店对文具进行组合销售,甲种组合:2支红色圆珠笔,4支黑色圆珠笔;乙种组合:3支红色圆珠笔,8支黑色圆珠笔,1个笔记本;丙种组合:2支红色圆珠笔,6支黑色圆珠笔,1个笔记本.已知红色圆珠笔每支2元,黑色圆珠笔每支1.5元,笔记本每个10元.某个周末销售这三种组合文具共485元,其中红色圆珠笔的销售额为116元,则笔记本的销售额为________元.
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)的图象交x轴于A(﹣2,0)和点B,交y轴负半轴于点C,抛物线对称轴为x=﹣![]() ,下列结论中,错误的结论是( )
,下列结论中,错误的结论是( )
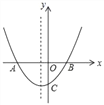
A. abc>0
B. 方程ax2+bx+c=0的解是x1=﹣2,x2=1
C. b2﹣4ac>0
D. a=b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,用篱笆靠墙围成矩形花围ABCD,墙可利用的最大长度为15米,一面利用旧墙,其余三面用篱笆围成,篱笆总长为24米.
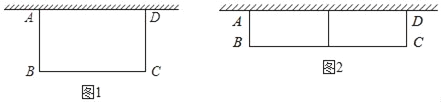
(1)若围成的花圃面积为40米2时,求BC的长;
(2)如图2若计划在花圃中间用一道隔成两个小矩形,且围成的花圃面积为50米2,请你判断能否成功围成花圃,如果能,求BC的长?如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
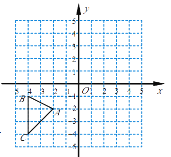
【题目】在平面直角坐标系中,△ABC各顶点的坐标分别为A(2,2),B(4,1),C(4,4).(正方形网格中每个小正方形的边长是 1个单位长度).
(1)画出将△ABC绕点O 顺时针旋转90度得到的△A1B1C1;
(2)写出A1、B1、C1的坐标;
(3)求出线段AC在旋转过程中所扫过的面积(结果保留![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
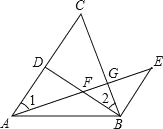
【题目】已知:如图,D是AC上一点,BE∥AC,BE=AD,AE分别交BD、BC于点F、G,且∠1=∠2.
(1)填空:图中与△BEF全等的三角形是______,与△BEF相似的三角形是_____(不再添加任何辅助线);
(2)对(1)中的两个结论选择其中一个给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,直线AE:
与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,直线AE:![]() 与抛物线相交于另一点E,点D为抛物线的顶点.
与抛物线相交于另一点E,点D为抛物线的顶点.
(1)求直线BC的解析式及点E的坐标;
(2)如图2,直线AE上方的抛物线上有一点P,过点P作PF⊥BC于点F,过点P作平行于![]() 轴的直线交直线BC于点G,当△PFG周长最大时,在
轴的直线交直线BC于点G,当△PFG周长最大时,在![]() 轴上找一点M,在AE上找一点N,使得
轴上找一点M,在AE上找一点N,使得![]() 值最小,请求出此时N点的坐标及
值最小,请求出此时N点的坐标及![]() 的最小值;
的最小值;
(3)在第(2)问的条件下,点R为抛物线对称轴上的一点,在平面直角坐标系中是否存在点S,使以点N,E,R,S为顶点的四边形为矩形,若存在,请直接写出点S的坐标,若不存在,请说明理由.
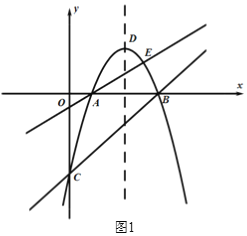
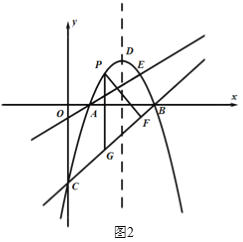
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在坐标平面内,三个顶点的坐标为A(0,3)、B(3,4)、C(2,2),(正方形网格中,每个小正方形边长为1个单位长度)
(1)画出△ABC向下平移4个单位得到的△A1B1C1;
(2)以B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比2:1,直接写出C2点坐标是 ;
(3)△A2BC2的面积是 平方单位.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,矩形DEFG的顶点G、F分别在AC、BC上,DE在AB上.
(1)求证:△ADG∽△FEB;
(2)若AG=5,AD=4,求BE的长.
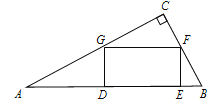
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节“赛龙舟,吃粽子”是中华民族的传统习俗.节日期间,小邱家包了三种不同馅的粽子,分别是:红枣粽子(记为A),豆沙粽子(记为B),肉粽子(记为C),这些粽子除了馅不同,其余均相同.粽子煮好后,小邱的妈妈给一个白盘中放入了两个红枣粽子,一个豆沙粽子和一个肉粽子;给一个花盘中放入了两个肉粽子,一个红枣粽子和一个豆沙粽子.
根据以上情况,请你回答下列问题:
(1)假设小邱从白盘中随机取一个粽子,恰好取到红枣粽子的概率是多少?
(2)若小邱先从白盘里的四个粽子中随机取一个粽子,再从花盘里的四个粽子中随机取一个粽子,请用列表法或画树状图的方法,求小邱取到的两个粽子中一个是红枣粽子、一个是豆沙粽子的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com