
【题目】如图,已知抛物线y=﹣x2+bx+C的图象过点A(﹣3,0),C(0,3).
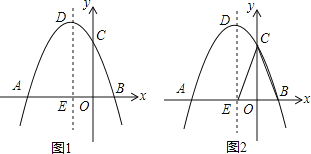
(1)求抛物线的解析式;
(2)探究:在抛物线的对称轴DE上是否存在点P,使得点P到直线AD和到x轴的距离相等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)探究:在对称轴DE左侧的抛物线上是否存在点F,使得2S△FBC=3S△EBC?若存在,求出点F的坐标;若不存在,说明理由.
【答案】(1)y=﹣x2﹣2x+3,(2)存在,P点坐标为(﹣1,![]() ﹣1)或(﹣1,﹣
﹣1)或(﹣1,﹣![]() ﹣1);(3)点F的坐标是(
﹣1);(3)点F的坐标是(![]() ,
,![]() ).
).
【解析】
试题分析:(1)把A、C两点坐标代入可求得b、c,可求得抛物线解析式;
(2)当点P在∠DAB的平分线上时,过P作PM⊥AD,设出P点坐标,可表示出PM、PE,由角平分线的性质可得到PM=PE,可求得P点坐标;当点P在∠DAB外角平分线上时,同理可求得P点坐标;
(3)可先求得△FBC的面积,过F作FQ⊥x轴,交BC的延长线于Q,可求得FQ的长,可设出F点坐标,表示出B点坐标,从而可表示出FQ的长,可求得F点坐标.
解:
(1)∵二次函数y=﹣x2+bx+c经过点A(﹣3,0),点C(0,3),
∴![]() ,解得
,解得![]() ,
,
∴抛物线的解析式y=﹣x2﹣2x+3,
(2)存在,
当P在∠DAB的平分线上时,如图1,作PM⊥AD,
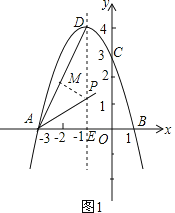
设P(﹣1,m),则PM=PDsin∠ADE=![]() (4﹣m),PE=m,
(4﹣m),PE=m,
∵PM=PE,
∴![]() (4﹣m)=m,m=
(4﹣m)=m,m=![]() ﹣1,
﹣1,
∴P点坐标为(﹣1,![]() ﹣1);
﹣1);
当P在∠DAB的外角平分线上时,如图2,作PN⊥AD,
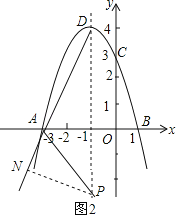
设P(﹣1,n),则PN=PDsin∠ADE=![]() (4﹣n),PE=﹣n,
(4﹣n),PE=﹣n,
∵PN=PE,
∴![]() (4﹣n)=﹣n,n=﹣
(4﹣n)=﹣n,n=﹣![]() ﹣1,
﹣1,
∴P点坐标为(﹣1,﹣![]() ﹣1);
﹣1);
综上可知存在满足条件的P点,其坐标为(﹣1,![]() ﹣1)或(﹣1,﹣
﹣1)或(﹣1,﹣![]() ﹣1);
﹣1);
(3)∵抛物线的解析式y=﹣x2﹣2x+3,
∴B(1,0),
∴S△EBC=![]() EBOC=3,
EBOC=3,
∵2S△FBC=3S△EBC,
∴S△FBC=![]() ,
,
过F作FQ⊥x轴于点H,交BC的延长线于Q,过F作FM⊥y轴于点M,如图3,

∵S△FBC=S△BQH﹣S△BFH﹣S△CFQ
=![]() HBHQ﹣
HBHQ﹣![]() BHHF﹣
BHHF﹣![]() QFFM
QFFM
=![]() BH(HQ﹣HF)﹣
BH(HQ﹣HF)﹣![]() QFFM
QFFM
=![]() BHQF﹣
BHQF﹣![]() QFFM
QFFM
=![]() QF(BH﹣FM)
QF(BH﹣FM)
=![]() FQOB
FQOB
=![]() ,
,
∴FQ=9,
∵BC的解析式为y=﹣3x+3,
设F(x0,﹣x02﹣2x0+3),
∴﹣3x0+3+x02+2x0﹣3=9,
解得:x0=![]() 或
或![]() (舍去),
(舍去),
∴点F的坐标是(![]() ,
,![]() ).
).


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】方成同学看到一则材料:甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地.设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示.
方成思考后发现了如图1的部分正确信息:乙先出发1h;甲出发0.5小时与乙相遇.
请你帮助方成同学解决以下问题:
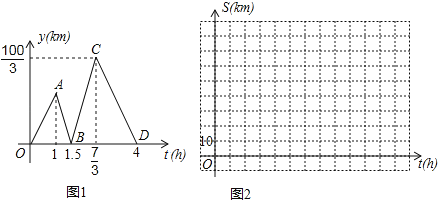
(1)分别求出线段BC,CD所在直线的函数表达式;
(2)当20<y<30时,求t的取值范围;
(3)分别求出甲,乙行驶的路程S甲,S乙与时间t的函数表达式,并在图2所给的直角坐标系中分别画出它们的图象;
(4)丙骑摩托车与乙同时出发,从N地沿同一公路匀速前往M地,若丙经过![]() h与乙相遇,问丙出发后多少时间与甲相遇?
h与乙相遇,问丙出发后多少时间与甲相遇?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com