练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．若两圆的半径分别为3和4，圆心距为2，则两圆的位置关系是相交．

    分析 先计算两半径之差与两半径之和，再把圆心距与它们比较大小，然后根据圆与圆的位置关系进行判断．

    解答 解：∵4-3=1，4+3=7，
    而1＜2＜7，
    ∴两圆的位置关系是相交．
    故答案为相交．

    点评 本题考查了圆与圆的位置关系：两圆的圆心距为d，两圆半径分别为R，r，则：两圆外离?d＞R+r；两圆外切?d=R+r；两圆相交?R-r＜d＜R+r（R≥r）；两圆内切?d=R-r（R＞r）；两圆内含?d＜R-r（R＞r）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    2．若x，y，z满足$\left\{\begin{array}{l}{2x+3y-5z=0}\\{4x-y-3z=0}\end{array}\right.$，且xyz≠0，则$\frac{2x-3y}{4y+2z}$=-$\frac{1}{6}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

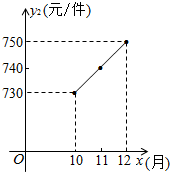    3．某企业为重庆计算机产业基地提供电脑配件．受美元走低的影响，从去年1至9月，该配件的原材料价格一路攀升，每件配件的原材料价格y1（元）与月份x（1≤x≤9，且x取整数）之间的函数关系如下表：
    月份x123456789
    价格y1（元/件）560580600620640660680700720
    随着国家调控措施的出台，原材料价格的涨势趋缓，10至12月每件配件的原材料价格y2（元）与月份x（10≤x≤12，且x取整数）之间存在如图所示的变化趋势：
    （1）请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识，直接写出y1 与x之间的函数关系式，根据如图所示的变化趋势，直接写出y2与x之间满足的一次函数关系式；
    （2）若去年该配件每件的售价为1000元，生产每件配件的人力成本为50元，其它成本30元，该配件在1至9月的销售量p1（万件）与月份x满足关系式p1=0.1x+1.1（1≤x≤9，且x取整数），10至12月的销售量p2（万件）p2=-0.1x+2.9（10≤x≤12，且x取整数）．求去年哪个月销售该配件的利润最大，并求出这个最大利润；
    （3）今年1至5月，每件配件的原材料价格均比去年12月上涨60元，人力成本比去年增加20%，其它成本没有变化，该企业将每件配件的售价在去年的基础上提高a%，与此同时每月销售量均在去年12月的基础上减少0.1a%．这样，在保证每月上万件配件销量的前提下，完成1至5月的总利润1700万元的任务，请你参考以下数据，估算出a的整数值．（参考数据：992=9801，982=9604，972=9409，962=9216，952=9025）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．已知有理数a、b、c在数轴上的位置如图，化简|a|-|a+b|+|c-a|．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．四边形ABCD中，已知AB=7，BC=5，CD=7，当AD=5时，四边形ABCD是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．（1）$\sqrt{1\frac{2}{3}}$÷2$\sqrt{2\frac{1}{3}}$×（-4$\sqrt{1\frac{2}{5}}$）       
    （2）$\frac{1}{\sqrt{2}}$-$\sqrt{6}$（$\sqrt{3}$-2$\sqrt{2}$）        
    （3）$\frac{\sqrt{3{a}^{2}}}{2b}$•$\sqrt{\frac{a}{b}}$÷2$\sqrt{\frac{2}{b}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．解方程组 
    （1）$\left\{\begin{array}{l}{3x-2y=6}\\{2x+3y=17}\end{array}\right.$               
    （2）$\left\{\begin{array}{l}{\frac{x+y}{2}+\frac{x-y}{2}=6}\\{4（x+y）-5（x-y）=2}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．如图，矩形ABCD中，AB=1，AC=2，对角线AC、BD相交于点O，直线EF过点O，交 BC于点E，交AD于点F．若四边形AECF恰好为菱形，则∠FOD=30°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．现将连续自然数1至2015按图中方式排成一个长方形阵列，用一个长方形框出16个数，如图：
    （1）图中框出的16个数的和是352；
    （2）在图中，要使长方形框出的16个数的和分别等于2000，2015，能否有可能？试说明理由；若有可能，请求出该长方形框出的16个数中的最小数和最大数．

    查看答案和解析>>

    同步练习册答案