【题目】任意选择电视的某一频道，正在播放动画片，这个事件是 事件．（填“必然”“不可能”或“不确定”）
科目：初中数学 来源： 题型：
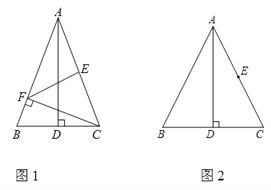
【题目】在锐角△ABC中，AB=AC，AD为BC边上的高，E为AC中点．
（1）如图1，过点C作CF⊥AB于F点，连接EF．若∠BAD=20°，求∠AFE的度数；
（2）若M为线段BD上的动点（点M与点D不重合），过点C作CN⊥AM于N点，射线EN，AB交于P点．
①依题意将图2补全；
②小宇通过观察、实验，提出猜想：在点M运动的过程中，始终有∠APE=2∠MAD．
小宇把这个猜想与同学们进行讨论，形成了证明该猜想的几种想法：
想法1：连接DE，要证∠APE=2∠MAD，只需证∠PED=2∠MAD．
想法2：设∠MAD=α，∠DAC=β，只需用α，β表示出∠PEC，通过角度计算得∠APE=2α．
想法3：在NE上取点Q，使∠NAQ=2∠MAD，要证∠APE=2∠MAD，只需证△NAQ∽△APQ．……
请你参考上面的想法，帮助小宇证明∠APE =2∠MAD．（一种方法即可）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图：已知点A、B是反比例函数y=﹣
上在第二象限内的分支上的两个点，点C（0，3），且△ABC满足AC=BC，∠ACB=90°，则线段AB的长为__．
查看答案和解析>>
科目：初中数学 来源： 题型：
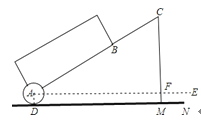
【题目】一种拉杆式旅行箱的示意图如图所示，箱体长AB=50cm，拉杆最大伸长距离BC=35cm，（点A、B、C在同一条直线上），在箱体的底端装有一圆形滚轮⊙A，⊙A与水平地面切于点D，AE∥DN，某一时刻，点B距离水平面38cm，点C距离水平面59cm．
（1）求圆形滚轮的半径AD的长；
（2）当人的手自然下垂拉旅行箱时，人感觉较为舒服，已知某人的手自然下垂在点C处且拉杆达到最大延伸距离时，点C距离水平地面73.5cm，求此时拉杆箱与水平面AE所成角∠CAE的大小（精确到1°，参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，某电视台的娱乐节目《周末打放送》有这样的翻奖牌游戏，数字的背面写有祝福语或奖金数，游戏规则是：每翻动正面一个数字，看看反面对应的内容，就可知是得奖还是得到温馨祝福．
1 | 2 | 3 |
4 | 5 | 6 |
7 | 8 | 9 |
正面
祝你开心 | 万事如意 | 奖金800元 |
身体健康 | 心想事成 | 奖金500元 |
奖金200元 | 生活愉快 | 谢谢参与 |
反面
计算：
（1）“翻到奖金800元”的概率；
（2）“翻到奖金”的概率；
（3）“翻不到奖金”的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读解题过程,回答问题.
如图,OC在∠AOB内,∠AOB和∠COD都是直角,且∠BOC=30°,求∠AOD的度数.
解:过O点作射线OM,使点M,O,A在同一直线上.
因为∠MOD+∠BOD=90°,∠BOC+∠BOD=90°,所以∠BOC=∠MOD,
所以∠AOD=180°-∠BOC=180°-30°=150°.
(1)如果∠BOC=60°,那么∠AOD等于多少度?如果∠BOC=n°,那么∠AOD等于多少度?
(2)如果∠AOB=∠DOC=x°,∠AOD=y°,求∠BOC的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列说法正确的有（ ） ①无理数是无限小数；②无限小数是无理数；③开方开不尽的数是无理数；④两个无理数的和一定是无理数；⑤无理数的平方一定是有理数．
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】规定※是一种新的运算符号，且a※b=ab+a+b，例如：2※3=2×3+2+3=11，那么（3※4）※1=（ ）
A.19
B.29
C.39
D.49
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
