
 在平面直角坐标系xOy中,抛物线y=x2-2mx+m2-1与x轴交于A,B两点(点A在点B左侧)
在平面直角坐标系xOy中,抛物线y=x2-2mx+m2-1与x轴交于A,B两点(点A在点B左侧)分析 (1)将抛物线配方成顶点式即可得顶点坐标;
(2)求出y=0时x的值即可得;
(3)由△OAC与△ABC等高且△OAC的面积小于△ABC的面积,知OA<AB,分点A在x轴的正半轴和点A在x轴的负半轴解答可得.
解答 解:(1)y=x2-2mx+m2-1=(x-m)2-1,
∴顶点为(m,-1);
(2)令y=0
∴x2-2mx+m2-1=0
解得:x1=m-1,x2=m+1,
∵点 A在点B的左侧,
∴A(m-1,0),B(m+1,0),
∴AB=(m+1)-( m-1 )=2;
(3)∵△OAC与△ABC等高
△OAC的面积小于△ABC的面积
∴OA<AB,
①当点A在x轴的正半轴上时,
如图1,
则m-1<2,解得:m<3;
②当点A在x轴的负半轴上时,
则1-m<2,解得:m>-1,
又∵点C不与原点O重合,
∴m 2-1≠0,m≠±1,
∴-1<m<3且 m≠1.
点评 本题主要考查抛物线与x轴的交点问题,熟练掌握二次函数的图象和性质及分类讨论思想的运用是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
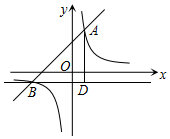 如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(1,3)和B(-3,m).
如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(1,3)和B(-3,m).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
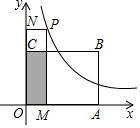 如图,矩形OABC的四个顶点分别为O(0,0),A(2,0),B(2,1),C(0,1),P(x,y)是反比例函数y=$\frac{1}{x}$(x>0)图象上的一个动点,过点P作PM⊥x轴,PN⊥y轴,M、N为垂足,记矩形OMPN与矩形OABC的重叠部分面积为S,则S与x轴的函数关系式的图象为( )
如图,矩形OABC的四个顶点分别为O(0,0),A(2,0),B(2,1),C(0,1),P(x,y)是反比例函数y=$\frac{1}{x}$(x>0)图象上的一个动点,过点P作PM⊥x轴,PN⊥y轴,M、N为垂足,记矩形OMPN与矩形OABC的重叠部分面积为S,则S与x轴的函数关系式的图象为( )| A. | 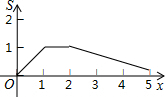 | B. | 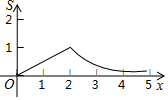 | ||
| C. | 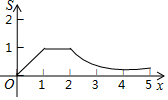 | D. | 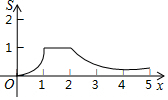 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 11 | D. | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
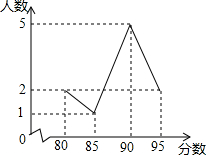 在学校演讲比赛中,10名选手的成绩折线统计图如图所示,则下列说法正确的是( )
在学校演讲比赛中,10名选手的成绩折线统计图如图所示,则下列说法正确的是( )| A. | 最高分90 | B. | 众数是5 | C. | 中位数是90 | D. | 平均分为87.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 人数 | 3 | 4 | 2 | 1 |
| 答对题数 | 4 | 5 | 7 | 8 |
| A. | 4和5 | B. | 5和4 | C. | 5和5 | D. | 6和5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com