
����Ŀ�����壺��ͼ1����![]() ���߶�
���߶�![]() �ָ��
�ָ��![]() ,����
,����![]() Ϊ�ߵ���������һ��ֱ�������Σ����
Ϊ�ߵ���������һ��ֱ�������Σ����![]() ���߶�
���߶�![]() �Ĺ��ɵ㡣
�Ĺ��ɵ㡣
(1)��֪��![]() ���߶�
���߶�![]() �Ĺ��ɵ㣬��
�Ĺ��ɵ㣬��![]() ,��
,��![]() �ij���
�ij���
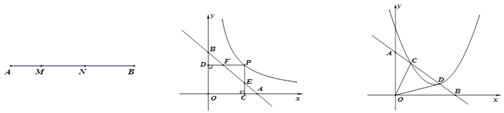
(ͼ1) ��ͼ2�� ��ͼ3��
(2)��ͼ2����![]() �Ƿ���������
�Ƿ���������![]() �ϵĶ��㣬ֱ��
�ϵĶ��㣬ֱ��![]() ��������ֱ���
��������ֱ���![]() ���㣬����
���㣬����![]() �ֱ���
�ֱ���![]() �������ߣ�����Ϊ
�������ߣ�����Ϊ![]() ���ҽ��߶�
���ҽ��߶�![]() ��
��![]() ����֤����
����֤����![]() ���߶�
���߶�![]() �Ĺ��ɵ㡣
�Ĺ��ɵ㡣
(3)��ͼ3����֪һ�κ���![]() �������ύ��
�������ύ��![]() ���㣬����κ���
���㣬����κ���![]() ����
����![]() ���㣬��
���㣬��![]() ���߶�
���߶�![]() �Ĺ��ɵ㣬��
�Ĺ��ɵ㣬��![]() ��ֵ��
��ֵ��
���𰸡�(1) ![]() ����
����![]() ;(2)������;(3)
;(2)������;(3) ![]()
��������������(1) ���������:�ٵ�MNΪ����߶�ʱ,�ɹ��ɶ������BN;�ڵ�BNΪ����߶�ʱ,�ɹ��ɶ������BN����;(2)��������ɵõ�A��B��E�����꣬���ó���BDF����PEF�� ��ACE��Ϊ����ֱ�������Σ���������֮��ľ��빫ʽ�ɵ�BF��AE��EF�ij����������![]() �Ӷ���֤;(3) ��C��CE��x����E��DF��x����F, ��C
�Ӷ���֤;(3) ��C��CE��x����E��DF��x����F, ��C![]() ��D
��D![]() ,�ɸ���ϵ���Ĺ�ϵ�����б�ʽ�ɵ�
,�ɸ���ϵ���Ĺ�ϵ�����б�ʽ�ɵ�![]() ����OE+OF=3��OB=3�ɵ�OE=BF���ɡ�BDF����PEF�� ��ACE��Ϊ����ֱ�������Σ��ɵ�AC=BD����AC=BD=a=
����OE+OF=3��OB=3�ɵ�OE=BF���ɡ�BDF����PEF�� ��ACE��Ϊ����ֱ�������Σ��ɵ�AC=BD����AC=BD=a=![]() ��EF=
��EF=![]() ���ɵ�m��ֵ.
���ɵ�m��ֵ.
��⣺��1�������⣬BNΪб��ʱ��BN=![]()
BNΪֱ�DZ�ʱ��BN=![]()
�� BN�ij�Ϊ![]() ����
����![]() .
.
��2����֪A��2,0����B��0,2����P��a,b��������֪E��a,-a+2�����ҡ�BDF����PEF�� ��ACE��Ϊ����ֱ��������.
�� BF=![]() =
=![]() ��AE=
��AE=![]() ��EF=
��EF=![]()
�����![]() ,��E��F���߶�AB�Ĺ��ɵ�.
,��E��F���߶�AB�Ĺ��ɵ�.
��3�������⣬��C��DΪA��B�Ĺ��ɵ㣬����C��D����A��B֮��,
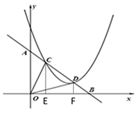
��C��CE��x����E��DF��x����F��
�����⣬��C![]() ��D
��D![]()
����![]() ,��
,��![]()
��![]()
![]() ,
,
��![]()
![]()
��OE+OF=3
�֡�OF+BF=3 ��OE=BF
����AC��CD��BDΪб�ߵ����������ζ�Ϊ����ֱ�������Ρ�
�� AC=BD
�����������![]() ��
��![]() ,
,
��AC=BD=a,��CD=![]() ����AB=
����AB=![]()
��![]()
��EF=![]() ,
,
��![]()
���![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
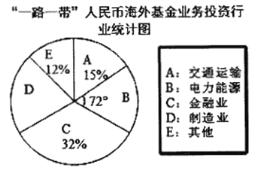
����Ŀ����һ·һ��������6���ˣ�����ǰΪֹ���й�����126�����Һ�29��������֯ǩ��174�ݺ����ļ���������һ·һ��������������ŷ���������ޡ���������̫������.��ֹ2019��һ����ĩ������Һ������ҵ���ģԼ3000��Ԫ����Ͷ�ʷ�Χ���ǽ�ͨ���䡢������Դ������ҵ������ҵ����Ҫ��ҵ��Ͷ����ҵͳ��ͼ��ͼ��ʾ��
��1����Ͷ������ҵ�Ļ���ԼΪ������Ԫ��
��2�����չ滮���й��������ԡ�һ·һ������������Ͷ�룬��2019��������ĩ��������Ͷ��630��Ԫ������ƽ��ÿ���ȵ���������ȣ���ƽ��ÿ���ȵ��������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
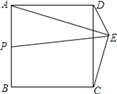
����Ŀ����ͼ��������![]() �ı߳�Ϊ4����
�ı߳�Ϊ4����![]() ����������һ���㣬
����������һ���㣬![]() ��
��![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() �˶�ʱ���߶�
�˶�ʱ���߶�![]() �����ֵΪ��������
�����ֵΪ��������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽ⱾУ���꼶ѧ����ĩ��ѧ����������ھ��꼶�����ȡ��һ����ѧ�� ����ĩ��ѧ�ɼ�Ϊ��������Ϊ A��90��100 �֣���B��80��89 �֣���C��60��79 �֣���D��0��59 �֣��ĸ��ȼ�����ͳ�ƣ�����ͳ�ƽ�����Ƴ�����ͳ��ͼ���������ͳ��ͼ������� ����.
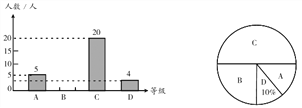
��1����������ȡ��ѧ�����ж����ˣ�
��2���벹ȫ����ͳ��ͼ��
��3�����ѧУ���꼶����ѧ�� 1200 �ˣ�������Ϊ 80 �֣��� 80 �֣�����Ϊ���㣬��� ����ξ��꼶ѧ����ĩ��ѧ���Գɼ�Ϊ�����ѧ��������Լ�ж��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AOΪRt��ABC�Ľ�ƽ���ߣ���ACB=90�㣬![]() ����OΪԲ�ģ�OC Ϊ�뾶��Բ�ֱ�AO��BC�ڵ�D��E������ED���ӳ���AC�ڵ�F��
����OΪԲ�ģ�OC Ϊ�뾶��Բ�ֱ�AO��BC�ڵ�D��E������ED���ӳ���AC�ڵ�F��
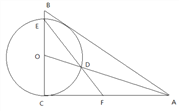
��1����֤��AB�ǡ�O�����ߣ�
��2����![]() ��ֵ��
��ֵ��
��3������O�İ뾶Ϊ4����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺�Ķ����в��ϣ���֪��������ʽ2x2+x+a��һ����ʽ�ǣ�x+2��������һ����ʽ�Լ�a ��ֵ
�⣺����һ����ʽ�ǣ�2x+b����
�������⣬��2x2+x+a=(x+2)(2x+b)��
չ������2x2+x+a =2x2+(b+4)x+2b��
����![]() �����
�����![]() ��
��
���ԣ���һ����ʽ�ǣ�2x3����a ��ֵ��6.
���������������������⣺��֪��������ʽ3x2 10x m ��һ����ʽ�ǣ�x+4��������һ����ʽ�Լ�m��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾����Ʒ���ع���ij������ˮ��ο��ҽ�����ߣ���Ʒ���ضԹ�������3000kg���ϣ���3000kg���Ĺ˿Ͳ����������۷���.������ÿǧ��9Ԫ���ɻ����ͻ����ţ��ҷ�����ÿǧ��8Ԫ���ɹ˿��Լ���˻�.��֪�ù�˾��ӻ��ص���˾���������Ϊ5000Ԫ.
��1���ֱ�д���ù�˾���ֹ���������y��Ԫ�����������ˮ����x��kg��֮��ĺ�����ϵʽ.
��2��������������һ��Χʱ��ѡ�����ֹ����������٣���˵������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y��kx+b��k��b�dz��������Ա���x��ȡֵΪ1��x��5ʱ����Ӧ�ĺ���ֵ�ķ�ΧΪ��2��y��2�����һ�κ����Ľ���ʽΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l1��y��x+n��2��ֱ��l2��y��mx+n�ཻ�ڵ�P��1��2����
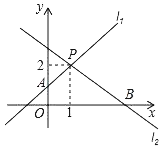
��1����m��n��ֵ��
��2������ͼ��ֱ��д������ʽmx+n��x+n��2�Ľ⼯��
��3����ֱ��l1��y�ύ�ڵ�A��ֱ��l2��x�ύ�ڵ�B�����ı���PAOB�������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com