
分析 (1)因为反比例函数f(x)=$\frac{k}{x}$(k>0)的定义域是[3,6],值域为[2,a],所以在第一象限,y随x的增加而减小,得到x=6时,y=2,推出k=12,当x=3时,y=$\frac{12}{x}$=4,即a=4.
(2)由于一次函数是递增或递减函数,所以当一次函数y=kx+b为增函数时,则x=-3,y=5;x=1,y=9当一次函数y=kx+b为减函数时,则x=-3,y=9;x=1,y=5,然后把它们分别代入y=kx+b中得到方程组,再解两个方程组即可.
(3)二次函数f(x)=x2+bx+c的定义域为[-4,2]值域为[6,10],对称轴x=-$\frac{b}{2}$,按照对称轴在x=-4的左边,在[-4,-1]内,在[-1,2]内,在x=2的右边,分别列出方程组即可解决问题.
解答 解:(1)∵反比例函数f(x)=$\frac{k}{x}$(k>0)的定义域是[3,6],值域为[2,a],
∴在第一象限,y随x的增加而减小,
∴x=6时,y=2,
∴k=12,
∴x=3时,y=$\frac{12}{x}$=4,
∴a=4.
(2)解:当x=-3,y=5;x=1,y=9,
∴$\left\{\begin{array}{l}{-3k+b=5}\\{k+b=9}\end{array}\right.$,
解方程组得$\left\{\begin{array}{l}{k=1}\\{b=8}\end{array}\right.$;
当x=-3,y=9;x=1,y=5,
∴$\left\{\begin{array}{l}{-3k+b=9}\\{k+b=5}\end{array}\right.$,
解方程组得$\left\{\begin{array}{l}{k=-1}\\{b=6}\end{array}\right.$,
∴函数的解析式为y=x+8或y=-x+6.
(3)存在.理由如下,
∵二次函数f(x)=x2+bx+c的定义域为[-4,2]值域为[6,10],对称轴x=-$\frac{b}{2}$,
∴当-$\frac{b}{2}$<-4时,$\left\{\begin{array}{l}{f(-4)=6}\\{f(2)=10}\end{array}\right.$⇒$\left\{\begin{array}{l}{16-4b+c=6}\\{4+2b+c=10}\end{array}\right.$⇒$\left\{\begin{array}{l}{b=2}\\{c=2}\end{array}\right.$(舍弃),
当-4≤-$\frac{b}{2}$≤-1时,$\left\{\begin{array}{l}{f(-\frac{b}{2})=6}\\{f(2)=10}\end{array}\right.$⇒$\left\{\begin{array}{l}{\frac{{b}^{2}}{4}-\frac{{b}^{2}}{2}+c=6}\\{4+2b+c=10}\end{array}\right.$⇒$\left\{\begin{array}{l}{b=-8}\\{c=22}\end{array}\right.$或$\left\{\begin{array}{l}{b=0}\\{c=6}\end{array}\right.$(舍弃),
当-1<-$\frac{b}{2}$≤2时,$\left\{\begin{array}{l}{f(-\frac{b}{2})=6}\\{f(-4)=10}\end{array}\right.$⇒$\left\{\begin{array}{l}{\frac{{b}^{2}}{4}-\frac{{b}^{2}}{2}+c=6}\\{16-4b+c=10}\end{array}\right.$⇒$\left\{\begin{array}{l}{b=4}\\{c=10}\end{array}\right.$或$\left\{\begin{array}{l}{b=12}\\{c=42}\end{array}\right.$(舍弃),
当-$\frac{b}{2}$>2时$\left\{\begin{array}{l}{f(-4)=10}\\{f(2)=6}\end{array}\right.$⇒$\left\{\begin{array}{l}{16-4b+c=10}\\{4+2b+c=6}\end{array}\right.$⇒$\left\{\begin{array}{l}{b=\frac{4}{3}}\\{c=-\frac{2}{3}}\end{array}\right.$(舍弃),
综上所述,满足条件的b、c的值为$\left\{\begin{array}{l}{b=4}\\{c=10}\end{array}\right.$或$\left\{\begin{array}{l}{b=4}\\{c=10}\end{array}\right.$.
点评 本题考查二次函数综合题、待定系数法求函数解析式、函数的增减性等知识,解题的关键是灵活运用待定系数法解决问题,学会用分类讨论的思想思考问题,把问题转化为方程组解决,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
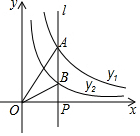 如图,直线l⊥x轴于点P,且与反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)及y2=$\frac{{k}_{2}}{x}$(x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为2,则k1-k2的值为( )
如图,直线l⊥x轴于点P,且与反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)及y2=$\frac{{k}_{2}}{x}$(x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为2,则k1-k2的值为( )| A. | 2 | B. | 3 | C. | 4 | D. | -4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,点A在y轴上,坐标为(0,3),点B在x轴上.
如图,在平面直角坐标系中,点A在y轴上,坐标为(0,3),点B在x轴上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com