
【题目】某工程队在我市实施棚户区改造过程中承包了一项拆迁工程.原计划每天拆迁![]() ,因为准备工作不足,第一天少拆迁了
,因为准备工作不足,第一天少拆迁了![]() .从第二天开始,该工程队加快了拆迁速度,第三天拆迁了
.从第二天开始,该工程队加快了拆迁速度,第三天拆迁了![]() .求:
.求:
![]() 该工程队第一天拆迁的面积;
该工程队第一天拆迁的面积;
![]() 若该工程队第二天、第三天每天的拆迁面积比前一天增加的百分数相同,求这个百分数.
若该工程队第二天、第三天每天的拆迁面积比前一天增加的百分数相同,求这个百分数.
【答案】(1)该工程队第一天拆迁的面积为1000m2;(2)该工程队第二天、第三天每天的拆迁面积比前一天增长的百分数是20%.
【解析】
试题(1)第一天拆迁面积=原计划的拆迁面积×(1-20%),把相关数值代入计算即可;
(2)等量关系为:第一天的拆迁面积×(1+百分数)2=第3天的拆迁面积,把相关数值代入计算即可.
(1)该工程队第一天拆迁面积是1250×(1-20%)=1000m2;
(2)设这个百分数是x,则
1000(1+x)2=1440,
(1+x)2=1.44,
1+x=±1.2,
x1=1.2-1=0.2=20%,x2=-1.2-1=-2.2.
经检验:x2=-2.2不合题意,舍去,只取x1=20%,
答:这个百分数是20%.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
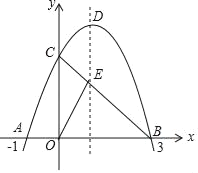
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E、D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)求点C和点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(k﹣1)x2+(2k﹣3)x+k+1=0有两个不相等的实数根.
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2﹣4x+k=0与x2+mx﹣1=0有一个相同的根,求此时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学课外兴趣小组成员在研究下面三个有联系的问题,请你帮助他们解决:
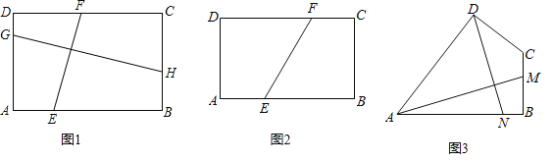
(1)如图1,矩形ABCD中,AB=a,BC=b,点E,F分别在AB,DC上,点G,H分别在AD,BC上且EF⊥GH,求![]() 的值.
的值.
(2)如图2,矩形ABCD中,AB=4,BC=3,将矩形对折,使得B、D重叠,折痕为EF,求EF的长.
(3)如图3,四边形ABCD中,∠ABC=90°,AB=AD=8,BC=CD=4,AM⊥DN,点M,N分别在边BC,AB上,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC边长为2,D为BC中点,连接AD.点O在线段AD上运动(不含端点A、D),以点O为圆心,![]() 长为半径作圆,当
长为半径作圆,当![]() O与△ABC的边有且只有两个公共点时,DO的取值范围为_____.
O与△ABC的边有且只有两个公共点时,DO的取值范围为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
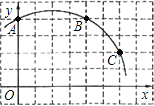
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)在图中确定该圆弧所在圆的圆心D点的位置,并写出点D点坐标为________.
(2)连接AD、CD,求⊙D的半径及![]() 的长;
的长;
(3)有一点E(6,0),判断点E与⊙D的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径OC=5cm,直线l⊥OC,垂足为H,且![]() 交⊙O于A、B两点,AB=8cm,则l沿OC所在直线平移后与⊙O相切,则平移的距离是( )
交⊙O于A、B两点,AB=8cm,则l沿OC所在直线平移后与⊙O相切,则平移的距离是( )
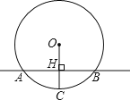
A.2cm或8cmB.2cmC.1cm 或8cmD.1cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com