解:(1)∵一次函数y=kx+2的图象与二次函数的图象交于y轴的A点,
∴A(0,2);
∵以CA为半径的⊙C与x轴相切,
∴点C在x轴上方,可设C(1,y),则有:
y
2=(1-0)
2+(y-2)
2,解得 y=

即:顶点C(1,

);
设二次函数的解析式为:y=a(x-1)
2+

,代入A(0,2),有:
a(0-1)
2+

=2,解得 a=

∴二次函数的解析式:y=

(x-1)
2+

=

x
2-

x+2.
(2)当x=3时,y=

(x-1)
2+

=

×4+

=

,即 B(3,

);
由(1)知,A(0,2),所以 AB的中点(

,
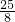
),AB=
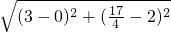
=
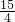
;
过点C且平行于x轴的直线l:y=

,所以以AB为直径的圆心到直线l的距离为:
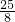
-

=
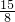
=

AB;
因此以AB为直径的圆与直线l相切.
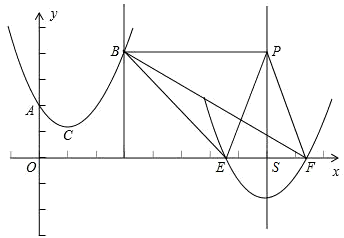
(3)二次函数平移后的解析式为y=

(x-8)
2+

-t,
令y=0,即

(x-8)
2+

-t=0,解得:x=8±

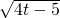
;
假设E(8-

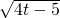
,0)、F(8+

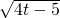
,0),EF的中垂线为x=8;
过B、E、F三点的圆心在x=8上,若过B、E、F三点的圆的面积最小,只需点B到直线x=8的距离最小,即最小值为5;
过B作直线x=8的垂线,垂足P即为圆心,半径r=5;
则PE=5,EF=
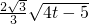
,ES=

EF=
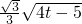
;
由PS
2+ES
2=PE
2,得:(

)
2+

(4t-5)=5
2,
解得:t=
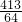
;
即:当t=
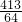
时,过B、E、F三点的圆的面积最小.
分析:(1)由于点A在y轴上,根据一次函数的解析式(主要注意常数项)即可得到点A的坐标,所以要求出二次函数的解析式,还必须知道顶点C的具体坐标;已知以C为半径的圆与⊙C相切,那么点C必在x轴的上方,且点C到x轴的距离(即C点的纵坐标值)与CA的长相同,可据此确定出点C的坐标;然后先将二次函数的解析式设为顶点式,再代入点A的坐标后可得解.
(2)已知点B的横坐标,代入(1)的二次函数解析式中可得到点B的坐标,以AB为直径的圆的圆心必为线段AB的中点,A点坐标已知,则圆心坐标可求,判定圆心到直线l的距离是否与AB长的一半相等即可.
(3)首先根据“左加右减,上加下减”的平移规律得出平移后的函数解析式,令函数值为0后可得到点E、F的坐标(用含t的式子表达);题目要求的是过B、E、F三点的圆的面积最小,那么这个圆的半径应该最小,可根据这个思路来解题;设这个圆的圆心为P,那么PB=PE=PF=r
P,所以点P必在线段EF的中垂线上,如果半径r
P最短,那么PB的长最短,通过图示我们可以看出,当BP垂直于EF的中垂线时(即BP为点B到EF中垂线的垂线段),BP的长最短,可据此确定圆心P的坐标,然后由PE=BP列方程求得t的值.
点评:此题是圆与函数的综合题,主要涉及了函数解析式的确定、函数图象的平移、直线与圆的位置关系、三角形的外接圆等重要知识点;题目的难点在于最后一题,将三角形外接圆的面积最小问题转化为半径长的问题是突破此题的关键所在.

 且A点在y轴上,以C为圆心,CA为半径的⊙C与x轴相切,
且A点在y轴上,以C为圆心,CA为半径的⊙C与x轴相切,
 );
); ,代入A(0,2),有:
,代入A(0,2),有: =2,解得 a=
=2,解得 a=
 (x-1)2+
(x-1)2+ =
= x2-
x2- x+2.
x+2. (x-1)2+
(x-1)2+ =
= ×4+
×4+ =
= ,即 B(3,
,即 B(3, );
); ,
,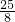 ),AB=
),AB=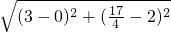 =
=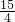 ;
; ,所以以AB为直径的圆心到直线l的距离为:
,所以以AB为直径的圆心到直线l的距离为: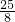 -
- =
=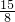 =
= AB;
AB; (3)二次函数平移后的解析式为y=
(3)二次函数平移后的解析式为y= (x-8)2+
(x-8)2+ -t,
-t, (x-8)2+
(x-8)2+ -t=0,解得:x=8±
-t=0,解得:x=8±
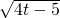 ;
;
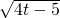 ,0)、F(8+
,0)、F(8+
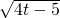 ,0),EF的中垂线为x=8;
,0),EF的中垂线为x=8;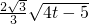 ,ES=
,ES= EF=
EF=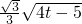 ;
; )2+
)2+ (4t-5)=52,
(4t-5)=52,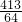 ;
;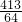 时,过B、E、F三点的圆的面积最小.
时,过B、E、F三点的圆的面积最小.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案 且A点在y轴上,以C为圆心,CA为半径的⊙C与x轴相切,
且A点在y轴上,以C为圆心,CA为半径的⊙C与x轴相切, (2006•河北区一模)如图,已知二次函数的顶点坐标为(2,0),直线y=x+2与该二次函数的图象交于A,B两点,其中A点在y轴上,
(2006•河北区一模)如图,已知二次函数的顶点坐标为(2,0),直线y=x+2与该二次函数的图象交于A,B两点,其中A点在y轴上,