

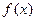 的奇偶性并证明;
的奇偶性并证明;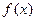 的定义域为[
的定义域为[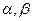 ](
](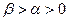 ),判断
),判断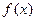 在定义域上的增减性,并加以证明;
在定义域上的增减性,并加以证明;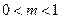 ,使
,使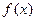 的值域为[
的值域为[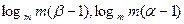 ]的定义域区间[
]的定义域区间[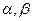 ](
](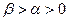 )是否存在?若存在,求出[
)是否存在?若存在,求出[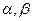 ],若不存在,请说明理由.
],若不存在,请说明理由. 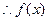 为奇函数
为奇函数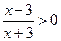 得
得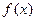 的定义域为
的定义域为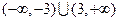 ,关于原点对称。
,关于原点对称。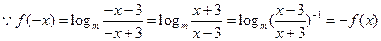
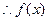 为奇函数 ………………………………3分
为奇函数 ………………………………3分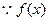 的定义域为[
的定义域为[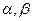 ](
](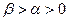 ),则[
),则[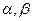 ]
]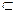
 。设
。设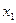 ,
,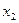
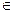 [
[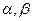 ],则
],则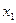
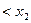 ,且
,且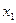 ,
,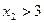 ,
,

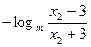 =
=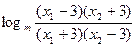 。。。。。。 5分
。。。。。。 5分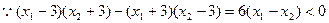 ,
,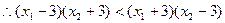 即
即 , 。。。。。。。。。。。6分
, 。。。。。。。。。。。6分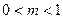 时,
时,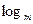
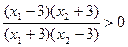 ,即
,即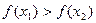 ; 。。。。。。。。。7分
; 。。。。。。。。。7分 时,
时,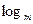
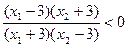 ,即
,即 , 。。。。。。。。。。8分
, 。。。。。。。。。。8分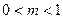 时,
时,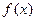 为减函数;
为减函数; 时,
时,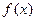 为增函数。 ………………………………9分
为增函数。 ………………………………9分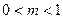 时,
时,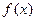 在[
在[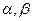 ]为递减函数,∴若存在定义域[
]为递减函数,∴若存在定义域[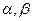 ](
](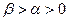 ),使值域为[
),使值域为[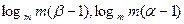 ],则有
],则有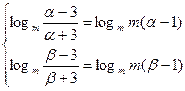 ……………………12分
……………………12分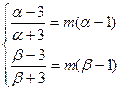 ∴
∴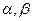 是方程
是方程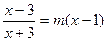 的两个解……………………13分
的两个解……………………13分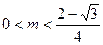 时,[
时,[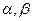 ]=
]=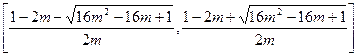 ,
,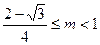 时,方程组无解,即[
时,方程组无解,即[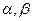 ]不存在。 ………………………14分
]不存在。 ………………………14分 

 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2013届上海市松江区九年级下学期3月月考数学试卷(带解析) 题型:解答题
(本题满分14分,其中第(1)题4分,第(2)题的第?、?小题分别为4分、6分)
如图1,在△ABC中,已知AB=15,cosB=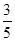 ,tanC=
,tanC=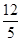 .点D为边BC上的动点(点D不与B、C重合),以D为圆心,BD为半径的⊙D交边AB于点E.
.点D为边BC上的动点(点D不与B、C重合),以D为圆心,BD为半径的⊙D交边AB于点E.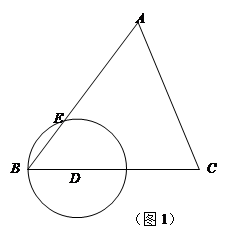
(1)设BD=x,AE=y,求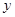 与
与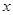 的函数关系式,并写出函数定域义;
的函数关系式,并写出函数定域义;
(2)如图2,点F为边AC上的动点,且满足BD=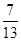 CF,联结DF.
CF,联结DF.
①当△ABC和△FDC相似时,求⊙D的半径;
② 当⊙D与以点F为圆心,FC为半径⊙F外切时,求⊙D的半径.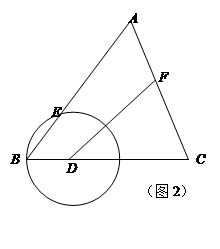
查看答案和解析>>
科目:初中数学 来源:2011-2012学年上海市松江区中考一模数学卷 题型:解答题
(本题满分14分,其中第(1)、(2)小题各4分,第(3)小题6分)已知:如图,在平面直角坐标系xOy中,二次函数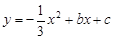 的图像经过点A(-1,1)和点B(2,2),该函数图像的对称轴与直线OA、OB分别交于点C和点D.
的图像经过点A(-1,1)和点B(2,2),该函数图像的对称轴与直线OA、OB分别交于点C和点D.
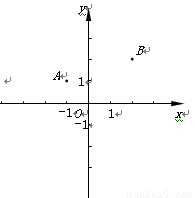
1.(1)求这个二次函数的解析式和它的对称轴;
2.(2)求证:∠ABO=∠CBO;
3.(3)如果点P在直线AB上,且△POB
与△BCD相似,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com