已知:抛物线y=ax2+(1-a)x+(5-2a)与x轴负半轴交于点A,与x轴正半轴交于点B,与y轴交于点C,tan∠CAO-tan∠CBO=2.
(1)当抛物线的解析式及顶点D的坐标;
(2)当线段OB与线段OC长度相等时,在抛物线的对称轴上取一点P,以点P为圆心作圆,使它与x轴和直线BD都相切,求点P的坐标.
分析:(1)先根据根与系数的关系,表示出OA、OB、OC的长,然后根据tan∠CAO-tan∠CBO=2即可得出关于a的方程,进而可求出a的值和抛物线的解析式.根据抛物线的解析式即可求出顶点D的坐标.
(2)本题可先设出P点的坐标,P点的横坐标为抛物线的对称轴的值,纵坐标的绝对值就是圆的半径,连接PF后可根据相似三角形DPF和DEB求出圆的半径的长,也就能求出P点的坐标.
解答:
解:(1)设A(x
1,0)、B(x
2,0)
依题意:x
1<0,x
2>0
并且x
1、x
2是关于x的方程ax
2+(1-a)x+(5-2a)=0的两个实数根
∴△=(1-a)
2-4a(5-2a)=9a
2-22a+1>0,x
1+x
2=
,
x
1x
2=
<0
①当点C在y轴正半轴上时,
∵C(0,5-2a)
∴OC=5-2a>0
∵tan∠CAO-tan∠CBO=2 tan∠CAO=
,tan∠CBO=
∴
-
=2
∵AO=-x
1,OB=x
2∴
-=2
∴
=2
∴
=2
解得:a=-1
当a=-1时符合题意
∴y=-x
2+2x+7,即顶点D(1,8)

②当点C在y轴负半轴上时,
∵C(0,5-2a)
∴CO=2a-5>0
∵tan∠CAO-tan∠CBO=2tan∠CAO=
,tan∠CBO=
∴
-=2
∵AO=-x
1,OB=x
2∴
-=2
∴
=2
∴
=2
解得:a=3
当a=3时符合题意
∴y=3x
2-2x-1,顶点D(
,-)
综上所述,抛物线的解析式为y=-x
2+2x+7或y=3x
2-2x-1,相应顶点D的坐标为(1,8)或(
,-)

(2)当抛物线的解析式为y=-x
2+2x+7时,B(1+2
,0),C(0,7),OB<OC,不合题意;
当抛物线的解析式为y=3x
2-2x-1时,B(1,0),C(0,-1),OB=CO
∴抛物线y=3x
2-2x-1符合题意(6分)
作PE⊥x轴于点E,PF⊥BD于点F.
设点P的坐标为(
,m)
顶点D
(,-),DB=,EB=∵⊙P与x轴、直线BD都相切
∴线段EP与线段FP长度相等
∵∠PDF=∠BDE,∠DFP=∠DEB
∴△DPF∽△DBE
∴
=
①当点P在第一象限时,m>0
∴
=
∴m=
∴P(
,
)
②当点P在第四象限时,点P一定在线段DE上,-
<m<0
∴
=
∴m=
∴P(
,
)
∴点P的坐标为P(
,
)或P(
,
).
点评:本题着重考查了一元二次方程根与系数的关系、切线的性质、三角形相似等知识点,综合性强,考查学生分类讨论,数形结合的数学思想方法.

 解:(1)设A(x1,0)、B(x2,0)
解:(1)设A(x1,0)、B(x2,0) ②当点C在y轴负半轴上时,
②当点C在y轴负半轴上时, (2)当抛物线的解析式为y=-x2+2x+7时,B(1+2
(2)当抛物线的解析式为y=-x2+2x+7时,B(1+2 ①当点P在第一象限时,m>0
①当点P在第一象限时,m>0

 发散思维新课堂系列答案
发散思维新课堂系列答案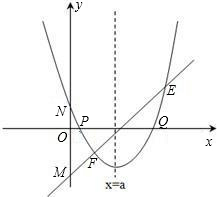 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由. (2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.
(2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.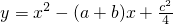 ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边. ,抛物线与x轴交于点P、Q,问是否
,抛物线与x轴交于点P、Q,问是否 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由. ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边.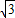 ,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.