
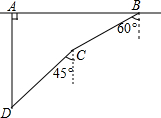
 如图,在一次军事演习中,蓝方在一条东西走向的公路上的A 处朝正南方向撤退,红方在公路上的B 处沿南偏西60°方向前进实施拦截.红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方.求红蓝双方最初相距多远(结果不取近似值).
如图,在一次军事演习中,蓝方在一条东西走向的公路上的A 处朝正南方向撤退,红方在公路上的B 处沿南偏西60°方向前进实施拦截.红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方.求红蓝双方最初相距多远(结果不取近似值). 分析 过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,则∠E=∠F=90°,红蓝双方相距AB=DF+CE.在Rt△BCE中,根据锐角三角函数的定义求出CE的长,同理,求出DF的长,进而可得出结论.
解答 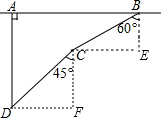 解:过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,则∠E=∠F=90°,红蓝双方相距AB=DF+CE.
解:过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,则∠E=∠F=90°,红蓝双方相距AB=DF+CE.
在Rt△BCE中,
∵BC=1000米,∠EBC=60°,
∴CE=BC•sin60°=1000×$\frac{\sqrt{3}}{2}$=500$\sqrt{3}$米.
在Rt△CDF中,
∵∠F=90°,CD=1000米,∠DCF=45°,
∴DF=CD•sin45°=1000×$\frac{\sqrt{2}}{2}$=500$\sqrt{2}$米,
∴AB=DF+CE=(500$\sqrt{2}$+500$\sqrt{3}$)米.
答:红蓝双方最初相距(500$\sqrt{2}$+500$\sqrt{3}$)米.
点评 本题考查了解直角三角形的应用-方向角问题,锐角三角函数的定义,正确理解方向角的定义,进而作出辅助线构造直角三角形是解题的关键.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:选择题
 如图,已知菱形ABCD,AC=8,BD=6,将此菱形绕点A逆时针旋转180°,则该菱形扫过的面积为( )
如图,已知菱形ABCD,AC=8,BD=6,将此菱形绕点A逆时针旋转180°,则该菱形扫过的面积为( )| A. | 32π | B. | 32π+24 | C. | 32π+48 | D. | 8π+24 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{19}{2}$ | B. | $\frac{21}{2}$ | C. | 7 | D. | 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
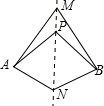 如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )
如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )| A. | AM=BM | B. | AP=BN | C. | ∠MAP=∠MBP | D. | ∠ANM=∠BNM |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com