
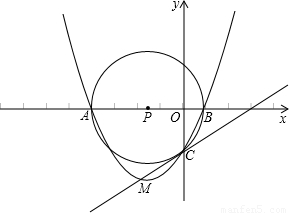
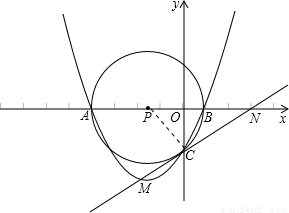
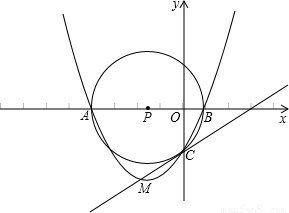
 解:(1)连接PC,
解:(1)连接PC, ,OP=4-
,OP=4- =
= .
.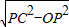 =
=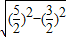 =2
=2
 (x-1)(x+4),
(x-1)(x+4), x2+
x2+ x-2.
x-2. x2+
x2+ x-2配方,得y=
x-2配方,得y= (x+
(x+ )2-
)2-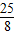 ,
, ,-
,-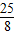 ).
).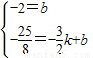 ,
,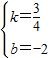 .
. x-2.
x-2. x-2中,令y=0,得x=
x-2中,令y=0,得x= .
. ,PN=
,PN= +
+ =
=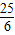 ,CN=
,CN=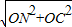 =
=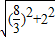 =
=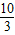 .
.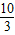 )2+(
)2+( )2=(
)2=(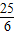 )2=PN2.
)2=PN2.

科目:初中数学 来源:2007年山东省烟台市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2010年四川省成都地区最新中考数学模拟题(六)(解析版) 题型:解答题
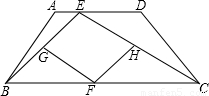 ),G、F、H分别是BE、BC、CE的中点.
),G、F、H分别是BE、BC、CE的中点.查看答案和解析>>
科目:初中数学 来源:2007年山东省烟台市中考数学试卷(解析版) 题型:选择题
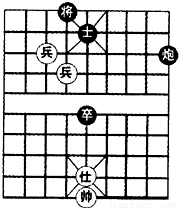 (2007•烟台)如图是中国象棋的一盘残局,如果用(4,0)表示“帅”的位置,用(3,9)表示“将”的位置,那么“炮”的位置应表示为( )
(2007•烟台)如图是中国象棋的一盘残局,如果用(4,0)表示“帅”的位置,用(3,9)表示“将”的位置,那么“炮”的位置应表示为( )查看答案和解析>>
科目:初中数学 来源:2006年浙江省嘉兴市中考数学试卷(课标卷)(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com