
 如图,一张矩形纸片ABCD中,AD>AB将矩形纸片ABCD沿过点A的直线折叠,使点D落到BC边上的点D′,折痕AE交DC于点E.
如图,一张矩形纸片ABCD中,AD>AB将矩形纸片ABCD沿过点A的直线折叠,使点D落到BC边上的点D′,折痕AE交DC于点E.分析 (1)以AD长为半径画弧与BC交于点D′,再做出∠DAD′的平分线,即可得出符合要求的图形;
(2)利用勾股定理以及翻折变换性质得出DE=D′E=x,EC=4-x,进而得出即可;
②过D′作CB的垂线交AE于F,根据翻折变换的性质可知,F即为所求,证明△ABG∽△FD′G,根据相似三角形的性质列出比例式,求出FD′的值,得到FD的长.
解答 解:(1)如图所示: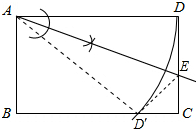
(2)①∵AD=5,AB=4,
∴AD′=5,
∴BD′=$\sqrt{AD{′}^{2}-A{B}^{2}}$=3,
∴CD′=5-3=2,
设DE=D′E=x,
则EC=4-x,
故EC2+D′C2=D′E2,
即(4-x)2+22=x2,
解得:x=$\frac{5}{2}$,
故ED的长为:$\frac{5}{2}$.
②如图所示,过D′作CB的垂线交AE于F,
由翻折变换的性质可知,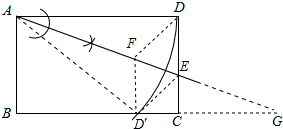 DF=FD′,
DF=FD′,
分别延长AE,BC相交于点G,
∵AD平行于CB,
∴∠DAG=∠AGC,
∵∠DAG=∠D′AG,AGC=∠D′AG,
∴GD′=AD′=AD=5,
∵D′F⊥CB,
∴FD′∥AB,
∴△ABG∽△FD′G,
∵Rt△ABD′中,AD′=5,AB=4,
∴BD′=3,BG=BD′+D′G=3+5=8,
∴△ABG与△FD′G的相似比为8:5,
∴AB:FD′=8:5,
∵AB=4,
∴FD′=2.5,即FD=2.5.
点评 此题主要考查了图形的翻折变换以及勾股定理和基本作图,熟练应用翻折变换图形翻折前后图形不变是解决问题的关键.


 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直角坐标系中的网格由单位正方形构成.△ABC中,A点坐标为(2,3)、B(-2,0)、C(0,-1).
如图,直角坐标系中的网格由单位正方形构成.△ABC中,A点坐标为(2,3)、B(-2,0)、C(0,-1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com