练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    请在下列四个2×2的方格中，各画出一个三角形，要求所画三角形与图中三角形组成的图形是轴对称图形，且所画三角形顶点与方格中的小正方形顶点重合，并将所画三角形涂上阴影．（注：所画的四个图形不能重复）

       


    画对1个得2分，全对得10分

     



    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    已知，如图，点B、F、C、E在同一直线上，AC、DF相交于点G，AB⊥BE，垂足为B，DE⊥BE，垂足为E，且AB＝DE，BF＝CE。

    求证：（1）△ABC≌△DEF；

     （2）GF＝GC。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    解方程组                    

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    等腰△ABC中，AB=AC=10 cm，BC=12 cm，则BC边上的高是       cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，∠MON=30o，点A1、A2、A3 …在射线ON上，点B1、B2、B3…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形，若OA1=1，则△A6B6A7 的边长为   ．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    （ 1）如图1，已知：在△ABC中，∠BAC＝90°，AB=AC，直线m经过点A，BD⊥直线m， CE⊥直线m，垂足分别为点D、E．证明：DE=BD+CE．

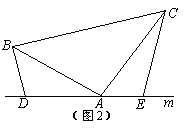
    （2）如图2，将(1)中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=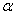，其中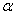为任意锐角或钝角．请问结论“DE=BD+CE”是否成立?如成立，请你给出证明；若不成立，请说明理由．

    （3）如图3，D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，试判断△DEF的形状．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    对于sin60°有下列说法：①sin60°是一个无理数；②sin60°>sin50°；③sin60°=6sin10°。其中说法正确的有（   ）

    A．0个

    B．1个

    C．2个

    D．3个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，小敏同学想测量一棵大树的高度．她站在B处仰望树顶，测得仰角为30°，再往大树的方向前进4m，测得仰角为60°，已知小敏同学身高（AB）为1.6m，则这棵树的高度为（结果精确到0.1m，≈1.73）．

    A．3.5m      B．3.6m       C．4.3m               D．5.1m

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    当x=1时，代数式x2+1=　     　．

    查看答案和解析>>

    同步练习册答案