
【题目】如图,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC. 
(1)求证:BC平分∠PBD;
(2)求证:BC2=ABBD;
(3)若PA=6,PC=6 ![]() ,求BD的长.
,求BD的长.
【答案】
(1)证明:连接OC,
∵PD为圆O的切线,
∴OC⊥PD,
∵BD⊥PD,
∴OC∥BD,
∴∠OCB=∠CBD,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠CBD=∠OBC,
则BC平分∠PBD

(2)证明:连接AC,
∵AB为圆O的直径,
∴∠ACB=90°,
∵∠ACB=∠CDB=90°,∠ABC=∠CBD,
∴△ABC∽△CBD,
∴ ![]() ,即BC2=ABBD
,即BC2=ABBD
(3)解:∵PC为圆O的切线,PAB为割线,
∴PC2=PAPB,即72=6PB,
解得:PB=12,
∴AB=PB﹣PA=12﹣6=6,
∴OC=3,PO=PA+AO=9,
∵△OCP∽△BDP,
∴ ![]() ,即
,即 ![]() ,
,
则BD=4.
【解析】(1)连接OC,由PD为圆O的切线,利用切线的性质得到OC垂直于PD,由BD垂直于PD,得到OC与BD平行,利用两直线平行得到一对内错角相等,再由OC=OB,利用等边对等角得到一对角相等,等量代换即可得证;(2)连接AC,由AB为圆O的直径,利用直径所对的圆周角为直角得到△ABC为直角三角形,根据一对直角相等,以及第一问的结论得到一对角相等,确定出△ABC与△BCD相似,由相似得比例,变形即可得证;(3)由切割线定理列出关系式,将PA,PC的长代入求出PB的长,由PB﹣PA求出AB的长,确定出圆的半径,由OC与BD平行得到△PCO与△DPB相似,由相似得比例,将OC,OP,以及PB的长代入即可求出BD的长.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图所示,P是直线l外一点,点A、B、C在l上,且PB⊥l,下列说法:①PA、PB、PC这3条线段中,PB最短;②点P到直线l的距离是线段PB的长;③线段AB的长是点A到PB的距离;④线段PA的长 是点P到直线l的距离.其中正确的是( )

A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,直线AB∥CD,E是AB与AD之间的一点,连接BE,CE,可以发现∠B+∠C=∠BEC.

证明过程如下:
证明:过点E作EF∥AB,
∵AB∥DC,EF∥AB(辅助线的作法),
∴EF∥DC
∴∠C=∠CEF.
∵EF∥AB,∴∠B=∠BEF
∴∠B+∠C=∠CEF+∠BEF
即∠B+∠C=∠BEC.
(2)如果点E运动到图②所示的位置,其他条件不变,∠B,∠C,∠BEC又有什么关系?并证明你的结论;
(3)如图③,AB∥DC,∠C=120°,∠AEC=80°,则∠A= .(写出结论,不用写计算过程)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )

A. ∠M=∠N B. AM=CN C. AB=CD D. AM∥CN
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三个天平的托盘中形状相同的物体质量相等.图①、图②所示的两个天平处于平衡状态,要使第三个天平也保持平衡,可在它的右盘中放置( )

A. 3个球 B. 4个球
C. 5个球 D. 6个球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,把△ABC 纸片沿 DE 折叠,使点 A 落在四边形 BCED 的内部点 A′的位置,试说明 2∠A=∠1+∠2;
(2)如图②,若把△ABC 纸片沿 DE 折叠,使点 A 落在四边形 BCED 的外部点A′的位置,写出∠A 与∠1、∠2 之间的等量关系(无需说明理由);
(3)如图③,若把四边形 ABCD 沿 EF 折叠,使点 A、D 落在四边形BCFE 的内部点 A′、D′的位置,请你探索此时∠A、∠D、∠1 与∠2 之间的数量关系,写出你发现的结论并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区为了进一步缓解交通拥堵问题,决定修建一条长为6千米的公路.如果平均每天的修建费y(万元)与修建天数x(天)之间在30≤x≤120,具有一次函数的关系,如下表所示.
X | 50 | 60 | 90 | 120 |
y | 40 | 38 | 32 | 26 |
(1)求y关于x的函数解析式;
(2)后来在修建的过程中计划发生改变,政府决定多修2千米,因此在没有增减建设力量的情况下,修完这条路比计划晚了15天,求原计划每天的修建费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,给出下列结论: ①2a+b>0;②b>a>c;③若﹣1<m<n<1,则m+n<﹣ ![]() ;④3|a|+|c|<2|b|.
;④3|a|+|c|<2|b|.
其中正确的结论是(写出你认为正确的所有结论序号).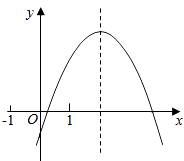
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D是边AC上一点,BC=BD=AD,则∠A的大小是( ).

A. 36° B. 54° C. 72° D. 30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com